Lectura Obligatoria: Barbara Ryden (Capítulo 11)
Lectura Sugerida:
-
Hasta ahora tenemos un modelo cosmológico muy exitoso que explica 1) la expansión de Hubble,
2) el fondo de radiación cósmico, y 3) la abundancia de los elementos primordiales.
A pesar del éxito del modelo del Big Bang caliente hay 2 problemas: el problema de porqué
Ω es tan cercano a 1 (flatness problem) y el
problema del horizonte.
- Como puede la inflación resolver el problema Ω tan cercano a 1?
La ecuación de Friedmann da la evolución del parámetro de curvatura (capitulo 3, sec. II):

Durante la inflación causada por una constante cosmológica constante, H se mantiene constante y a(t) crece exponencialmente, por lo cual la diferencia entre Ω y 1 decrece exponencialmente:

Si comparamos el parámetro de densidad antes y después de la inflación:

Suponiendo que antes de la inflación el Universo parte con una curvatura pronunciada |1-Ω(ti)|~1, al final de la inflación tenemos:

Vemos que el Universo termina siendo increíblemente plano luego de la inflación. Para satisfacer la observacion actual |1-Ω0|<0.2, se requiere N>60.
- Cómo puede la inflación resolver el problema del horizonte?
En general, la distancia al horizonte en un instante t cualquiera es (Cap 2, Sec VI):

Antes de la inflación el Universo estaba dominado por la radiación:

Al final de la inflación:

Para N ciclos de expansión:

Para el modelo de inflación en que ti=10-36 s y Hi~1036 s, la distancia al horizonte justo antes de la inflación es:

Para el modelo con N=100, la distancia al horizonte justo después de la inflación es:

El resultado neto de la inflación es que el tamaño del horizonte crece en un factor eN. En ausencia de inflacion el tamaño del horizonte en el momento del ultimo scatterinng (CMB) seria 0.4 Mpc. En cambio con inflacion esta distancia es 3×1017 Mpc.
La distancia propia actual a la superficie del CMB es de 14.000 Mpc. En el momento del ultimo scattering la parte actualmente visible del Universo estaba concentrada en 12 Mpc (14000/1100 Mpc), lo cual es mucho menor que el tamaño del horizonte de 3×1017 Mpc → todo el Universo observable (incluyendo el CMB) estuvo en contacto causal.
Otra manera de ver que el CMB estuvo en contacto causal: consideremos la distancia propia actual a la superficie del CMB (ultimo scattering):

Si la inflación terminó en tf=10-34 s, lo cual corresponde a af~2×10-27, en el instante justo después de la inflación el CMB que se observa hoy día estuvo contenido es una esfera de radio propio:

Justo antes de la inflación el Universo actualmente visible estaba contenido es una esfera de radio propio:

Esta distancia es 16 órdenes de magnitud más pequeña que el tamano del horizonte antes de la inflación (2cti=6×10-28 m) → el Universo que vemos hoy día tuvo todo el tiempo de alcanzar el equilibrio térmico antes de comenzar la inflación.
IV. El origen de la inflación La inflación resuelve dos problemas de la cosmología pero crea otros problemas: qué mecanismo gatilla la inflación y qué mecanismo la detiene? Necesitamos algo que se parezca a Λ. Cual es el tipo de fluido que logra esto?
En teoría cuántica de campos hay sustancias denominadas campos escalares que se comportan como constante cosmológica. El bosón de Higgs demuestra la existencia de campos escalares cuánticos.
En general, un campo escalar es una cantidad física con unidades de energía, presente en el espacio y el tiempo: Φ(r,t), que no depende de la dirección, y tiene asociada una energía potencial V(Φ). En nuestro caso, interesa un campo escalar uniforme que respete el principio corpernicano y que no dependa de la posicion, i.e., Φ(t).
V(Φ) tiene unidades de densidad de energía y es función de la intensidad del campo.
La densidad de energía y la presión de esta sustancia están determimados por Φ:


Esto es análogo al campo electromagnético con una densidad de energía asociada ρ=1/2(dE/dt)2 + 1/2(dB/dt)2 (acá V(Φ)=0).
Para que el campo escalar se comporte como una constante cosmológica, se requiere:

Para que esta condición se cumpla el campo escalar debe cambiar lento con el tiempo:

Un campo que se mantenga muy constante en el tiempo y V(Φ) domine la densidad de energía se denomina inflatón y actúa como una constante cosmológica.
Bajo qué cincunstancias se cumplen estas condiciones? Para esto hay que examinar la ecuación del fluido para el inflatón (Cap 3, Sec III):

Sustituyendo las expresiones anteriores para la densidad de energía y presión del inflatón:

Notar la analogía con la ecuación de Newton que describe el movimiento de una partícula acelerada en un potencial y con una fuerza de roce (d2x/dt2 + dx/dt + dV/dx = 0). Acá tenemos una fuerza proporcional a dV/dΦ y un roce proporcional a la expansión del Universo. A medida que el inflaton baja por el potencial la energia perdida la absorbe el espacio-tiempo para expandirse y alcanza una "velocidad terminal":

Cuando el inflatón alcanza la velocidad terminal, el requisito para que se comporte como constante cosmológica se traduce en:

Si el universo se encuentra en expansión exponencial debido al inflatón, el parámetro de Hubble es:

y la condición que debe cumplir el potencial es:


en donde EP=√hc5/2πG es la energía de Planck. Si la pendiente del potencial es suficientemente pequeña y la amplitud del potencial es suficientemente grande, entonces el inflatón puede dar lugar a una expansión exponencial.

Ejemplo de inflatónSi el inflatón comienza cuando Φ~0 y V(Φ)=V0, va a descender lentamente por un "plateau" con una pendiente

y va a contribuir con una densidad de energía εΦ~V0 ~ constante. El "plateau" es un "falso vacío" que no es realmente estable y el verdadero vacío ocurre en el mínimo cuando Φ=Φ0. La etapa inflacionaria dura mientras el inflatón desciende por el plateau, producendo una expansión exponencial con un parámetro de Hubble:

Habitualmente se asocia el inicio de la inflación a una hipotética etapa de gran unificación (GUT) posteriormente a la cual se separaron las fuerzas nucleares fuertes de las electrodébiles, a ti=10-36 s, pero tambien son aceptables modelos que hayan ocurrido a otras epocas tempranas, e.g. ti=10-20 s
La duración de la etapa inflacionaria va a depender de la duración del plateau y la forma exacta de V(Φ) hasta alcanzar el mínimo del potencial. Mientras mayores sean Φ0 y V0 o menor sea dV/dΦ, mayor será el número de ciclos de expansión exponencial.
Al final de la inflacion el Universo termina con una densidad de particulas muy baja y por tanto con una temperatura muy fria. Sin embargo, a medida que el inflaton desciende del plateau, la enorme densidad de energia potencial se libera, dando origen a oscilaciones en torno al minimo. En cada oscilacion el campo decae en particulas muy masivas (inflatones) y su acoplamiento con los campos del modelo estandar permite que se produzcan particulas mas livianas (quarks y fotones) a partir de los inflatones. Este proceso incrementa enormemente la densidad de la materia y la radiacion con un consiguiente "recalentamiento" del Universo. El periodo inflacionario termina cuando la enorme densidad de energía del inflatón se ha convertido en partículas y radiación y la expansión continua a una tasa más lenta dominada por la energía de la radiación.
Mientras el campo esta en el plateau surgen efectos cuanticos ya que el principio de incertidumbre impide conocer la posicion del campo de manera univoca en el tiempo y el espacio. Esto introduce oscilaciones del campo en distintas partes del Universo. Estas fluctuaciones cuanticas, que se manifiestan en el Fondo de Radiacion Cosmico, daran origen posteriormente a la formacion de estructuras del Universo.
Al mirar el cielo, estamos viendo la mecanica cuantica proyectada en la boveda celeste!
mhamuy@das.uchile.cl
La curvatura espacial está dada por la ecuación de Friedmann (Cap 3, Sec II):

En el instante actual:

Las mediciones del CMB y de las supernovas indican que Ω es muy cercano a 1:

La Relatividad General no restringe el valor de Ω y resulta curioso que el valor medido esté tan cerca de 1. Podría haber tenido el valor 1016 o 10-16 sin violar ninguna ley física. Podríamos argumentar que coincidentalmente las condiciones iniciales del Universo produjeron Ω0~1. Después de todo Ω0=0.8 o Ω0=1.2 no son tan cercanos a 1. Sin embargo, al extrapolar Ω hacia el pasado, la cercanía de Ω a 1 se hace más y más difícil de entender como una simple coincidencia. Veamos como evoluciona Ω en el tiempo.
Combinando las dos ecuaciones anteriores:

Durante la época en que la radiación y la materia dominaba, la constante de Hubble estaba dada por (Cap 5, inicio):

con lo cual:

A medida que el factor de escala (a) crecía, Ω se alejaba más y más de 1. Durante la época de radiación:

Durante la época de dominación de la materia:

Consideremos el caso benchmark: Ωr,0=8.4×10-5, Ωm,0=0.3±0.1, y ΩΛ,0=0.7±0.1. En el instante de la igualdad entre la materia y la radiación a z=3600 (a=1/3600) el parámetro de densidad era mucho más cercano a 1:

En el instante de la nucleosíntesis a=3.6×10-8 y el parámetro de densidad era aún mucho más cercano a 1:

Si nos remontamos al tiempo de Planck (el instante más temprano al que podemos acceder con la física conocida, t=5×10-44 s) el factor de escala era a=2×10-32 y el parámetro de densidad resulta extraordinariamente cercano a 1:

Nuestra existencia depende de este extraordinario ajuste fino ya que un cambio en Ω de sólo una parte en 30000 hubiese hecho que el Universo colapsara o se expandiera rápidamente sin haber dado la oportunidad para que se formaran las galaxias, las estrellas y los planetas. Podría ser una coincidencia, pero sería mucho más satisfactorio encontrar un mecanismo físico que aplanara el Universo temprano en vez de tener que acudir a condiciones iniciales tan caprichosas.
Durante la época del ultimo scattering (z~1100) el Universo está dominado por la materia y la distancia al horizonte dHor en esa época era aproximadamente 2c/H (Capítulo 4; Sec. IV). La ecuación de Friedmann (Cap. 5) se reduce a:
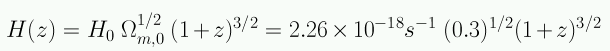
Para z=1100 se obtiene dHor=0.4 Mpc. La distancia angular al CMB es de dA=13 Mpc en el modelo benchmark, de modo que el tamaño angular del horizonte visto desde la Tierra es de θHor=20. El horizonte en la superficie del CMB se puede ver gráficamente:
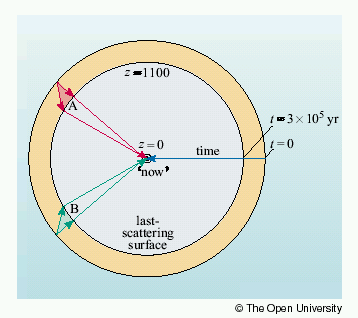
Dos regiones en la superficie del CMB separadas por más de 20 estaban fuera del horizonte de la otra y no pueden haber estado en comunicación física. Sin embargo, el CMB muestra variaciones de temperatura de apenas 10-5 a escalas mayores de 20.
Porqué distintas regiones del CMB que estaban fuera de contacto físico resultaron tan parecidas en sus propiedades físicas? El hecho que el CMB tenga la misma temperatura a escalas mayores que la distancia al horizonte se denomina el problema del horizonte. Es una coincidencia o existió un mecanismo físico que produjo esta homogeneidad global?

En 1981 Allan Guth propuso la teoría de la inflación con el fin de resolver el problema de porqué Ω es tan cercano a 1 y el problema del horizonte. La inflación es una expansión acelerada del Universo temprano producida por una constante cosmológica Λi. Una componente de este tipo tiene la propiedad de producir una densidad de energía constante y una presión negativa (Cap 3, Sec V):

En este caso la ecuación de aceleración es (Cap 3, Sec III):

Si Λ>0, la constante cosmológica implica una expansión acelerada. La ecuación de Friedmann (para k=0) es (Cap 4, Sec VI):


Si Λi se mantuvo constante durante la inflación Hi también se mantuvo constante y el factor de escala aumentó exponencialmente.
Para ver como la inflación puede resolver los tres problemas anteriores, supongamos que el Universo tuvo una expansión exponencial desde t=ti hasta t=tf en las épocas tempranas dominadas por la radiación. En este caso simple el factor de escala resulta ser:


Entre ti y tf el factor de escala creció en un factor:

Un posible modelo de inflación es el que comienza en ti=10-36 s, con un parámetro de Hubble Hi= 1/2cti = 0.5 x 1036 s-1, que duró N=100 ciclos de crecimiento exponencial (hasta tf=10-34 s), con lo cual obtenemos:

Para producir expansión exponencial con Hi~1036 s-1 se requiere una constante cosmológica con una densidad de energía:

Esta densidad es mucho mayor que la densidad de energía causada por la constante cosmológica actual.