Lectura Obligatoria: Barbara Ryden (Capítulo 3)
Lectura Sugerida: Peter Coles (Cosmology; Capítulo 2)
-
Queremos tener un modelo físico para describir la expansión cósmica. Existen cuatro fuerzas fundamentales
en la naturaleza: gravedad, electromagnetismo, fuerzas nucleares fuertes y fuerzas nucleares débiles.
Las fuerzas nucleares son de corto alcance por lo cual son despreciables a escalas cosmológicas.
Como los objetos astronómicos generalmente no poseen carga eléctrica neta, las fuerzas electromagnéticas
no juegan un rol a nivel global. Por estas razones la gravedad es la fuerza que domina la evolución del
Universo a gran escala y este es el marco teórico sobre el cual podemos construir modelos de Universo.
- 1. Todos los objetos permanecen en un estado de movimiento rectilíneo y uniforme a menos que actúe una fuerza sobre ellos
- 2. El cambio de momentum es proporcional a la fuerza y en la dirección de la fuerza aplicada (F=ma)
- 3. A cada acción hay una reacción de igual magnitud pero en la dirección opuesta
- La luz se curva en presencia de la gravedad (a pesar de que los fotones no tienen masa!!!) (confirmado por Eddington durante el eclipse solar de 1919)
- Como la luz se mueve en línea recta, entonces la curvatura se debe a que el espacio se curva y deja de ser Euclidiano en presencia de gravedad
- En RG masa y energía son equivalentes, por lo que la presencia de masa-energía en general causa la curvatura del espacio
- La gravedad afecta todo lo que posea energía
- Métrica para un espacio 2D plano (Euclidiano) en coordenas cartesianas:
ds2 = dx2 + dy2 (Teorema de Pitágoras) - Métrica para un espacio 2D plano en coordenas polares (ρ,φ):
ds2 = d ρ2 + ρ2dφ2 Notar que la métrica es invariante el cambio de coordenadas, i.e., un observador que use coordenadas cartesianas encontrará el mismo resultado que un observador que use coordenadas polares.
- Métrica isotrópica y esférica en 2D:
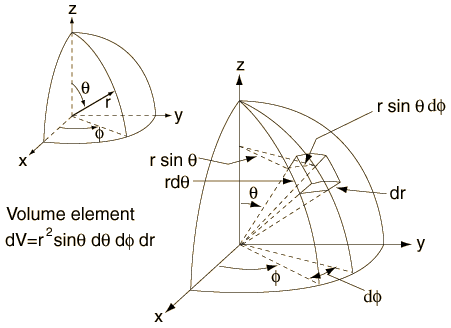
ds2 = R2 [ dθ2 + sin2θdφ2 ] (coordenadas esféricas) ds2 = dρ2 + R2 sin2(ρ/R) dφ2 (coordenada polares ρ=Rθ;φ) ds2 = dx2/[1-x2/R2] + x2 dφ2 (x=Rsinθ;φ) R: radio de la esfera
- Métrica isotrópica esférica, plana o hiperbólica en 2D:
ds2 = dρ2 + Sk2(ρ) dφ2 (coordenadas polares) Sk = R sin(ρ/R) (curvatura positiva) Sk = ρ (curvatura cero) Sk = R sinh(ρ/R) (curvatura negativa) También se puede escribir:
ds2 = dx2/[1-kx2/R2] + x2 dφ2 [x=Sk(ρ);φ] en que el parámetro de curvatura k puede ser:
k = +1 (curvatura positiva) k = 0 (curvatura cero) k = -1 (curvatura negativa) radio de curvatura : R
curvatura : 1/R2Resumen de propiedades geométricas de espacios de 2D CURVATURA NEGATIVA CERO POSITIVA ISOTROPICO SI SI SI PARAMETRO DE CURVATURA -1 0 +1 SUMA DE ANGULOS DE TRIANGULO ‹180 180 ›180 AREA ∞ ∞ 4πR2 MAXIMA SEPARACION ∞ ∞ πR NOMBRE ABIERTO PLANO CERRADO 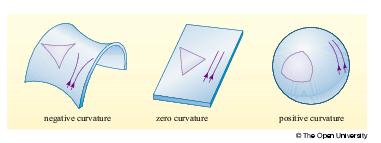
Haciendo una expansion de Taylor de Sk(ρ):
-
curvatura positiva: Rsin(ρ/R) = ρ [1 - (ρ/R)2/6] -> ρ (cuando ρ/R << 1)
curvatura negativa: Rsinh(ρ/R) = ρ [1 + (ρ/R)2/6] -> ρ (cuando ρ/R << 1)
El espacio parece plano cuando la curvatura es muy chica (R grande) o cuando el desplazamiento ρ es muy chico. - Métrica isotrópica en 3D:
Métrica para un espacio 3D plano (Euclidiano) en coordenas cartesianas:
ds2 = dx2 + dy2 + dz2 Métrica para un espacio 3D plano en coordenadas esféricas:
ds2 = dρ2 + ρ2 (dθ2 + sin2θ dφ2) Esta métrica se puede generalizar a espacios 3D con curvatura:ds2 = dρ2 + Sk2(ρ) (dθ2 + sin2θ dφ2) Definiendo: dΩ2 = (dθ2 + sin2θ dφ2)ds2 = dρ2 + Sk2(ρ) dΩ2 (coordenadas esféricas)
ds2 = dx2/[1-kx2/R2] + x2 dΩ2 
Visualización de un espacio curvo en 3DResumen de propiedades geométricas de espacios de 3D CURVATURA NEGATIVA CERO POSITIVA ISOTROPICO SI SI SI PARAMETRO DE CURVATURA -1 0 +1 SUMA DE ANGULOS DE TRIANGULO ‹180 180 ›180 VOLUMEN ∞ ∞ 2π2R3 MAXIMA SEPARACION ∞ ∞ FINITA NOMBRE ABIERTO PLANO CERRADO Notar que la curvatura es una propiedad de la grilla 3D y no requiere una cuarta coordenada (dimensión) espacial. Un observador en un espacio curvo está restringido a moverse dentro de los límites de las 3 dimensiones espaciales y no tiene ninguna noción de lo que ocurre afuera. NO EXISTE UN AFUERA.
- Métrica plana en espacio-tiempo (métrica de Minkowski)
ds2 = -c2dt2 + dρ2 + ρ2dΩ2 En el espacio-tiempo el desplazamiento de los fotones está dado por ds2 = 0, i.e, dρ/dt=±c
- En RG los efectos de la gravedad se traducen en cambios en las propiedades del espacio-tiempo.
El matemático y físico norte-americano Howard Robertson (1903-1961;
ver biografía)
y el matemático inglés Arthur Walker (1909-2001;
ver biografía)
demostraron independientemente (~1930) que la métrica más general que satisface
los principios de isotropía y homogeneidad es:
- a(t): factor de escala sin dimensión
- a(t0) = 1
- t: tiempo cósmico
- (ρ, θ, φ) coordenadas comóviles (constantes en el tiempo)
- (x, θ, φ) coordenadas comóviles (constantes en el tiempo)
- k: constante de curvatura (+1,0,-1)
- R0: radio de curvatura (km) en este instante t0
Conociendo a(t), k, y R0 sabemos toda la geometría
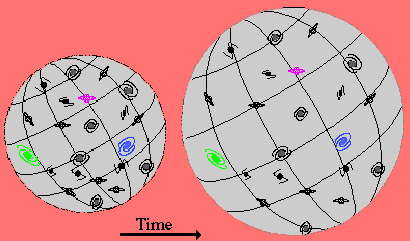
Modelo 2D de Universo isotrópico y homogéneo en expansión
- Jamás z + 1 !!!
- El redshift coresponde al aumento del factor de escala entre la emisión y la recepción.
El redshift es independiente de la historia de a(t). Sólo mide el cambio en a(t):

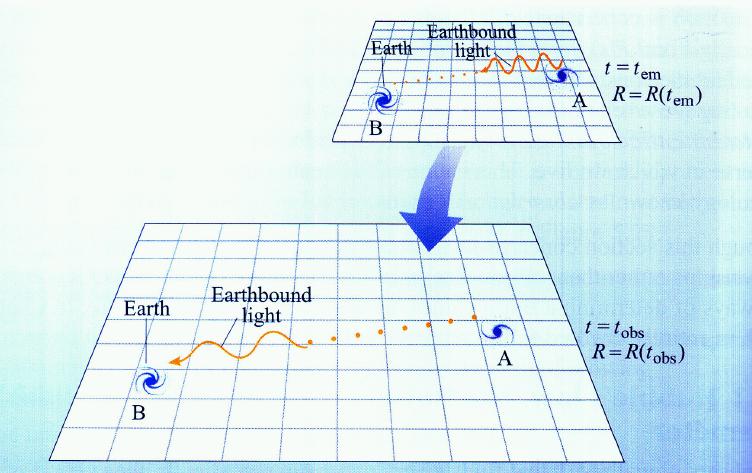
- El redshift se debe al estiramiento de las ondas causado por la expansión
del espacio y NO al efecto Doppler entre fuente y observador en un espacio estático.
-
Pregunta: Suponga que dos galaxias lejanas mantuvieron una distancia constante por un tiempo (etapa 1),
luego se alejaron por un período (etapa 2) y luego han mantenido la distancia constante (etapa 3).
Considere fotones emitidos por una de las galaxias en la etapa 1 y recibidos por la otra
galaxia en la etapa 3. Cual es el redshift medido por el observador que recibe los fotones
si el aumento de la distancia se debe a la expansión del espacio? Cual es el redshift si el
alejamiento se debió al aumento de la distancia en un espacio estático?
- El redshift hace que el espectro no sólo se desplace al rojo sino que se estire.
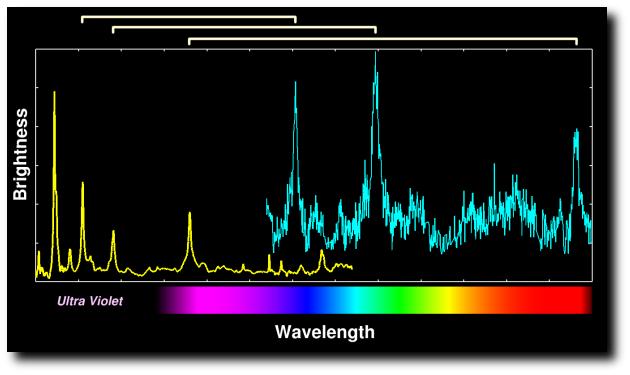
Espectro de un cuasar en reposo y otro corrido al rojo

- La luz de un objeto con redshift z=∞ fue emitida a te=0,
cuando el factor de escala a(te=0)=0.
mhamuy@das.uchile.cl
La Teoría Universal de la Gravitación fue originalmente presentada por Newton (1643-1727; biografía de Newton) en 1666 y fue reformulada por Einstein (1879-1955; biografía de Einstein) en 1915 (un cuarto de milenio más tarde) en su teoría de la Relatividad General.
Las leyes de Newton del movimiento:
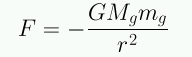
Según la 2a ley de Newton cada objeto posee una propiedad llamada masa inercial que resiste al cambio de momentum en respuesta a la aplicación de una fuerza:
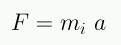
Si la fuerza de gravedad actúa sobre un objeto la aceleración resultante será:
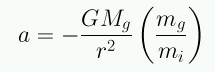
La masa gravitacional es la propiedad que determina la reacción de un objeto a la fuerza gravitacional producida por otro objeto, mientras que la masa inercial es la propiedad que determina la resistencia del objeto a la aceleración (debida a cualquier fuerza). La razón mg/mi podría variar de objeto a objeto. Sin embargo los experimentos de caída libre efectuados por Galileo demostraron que todos los objetos caen con la misma aceleración, independiente de su composición y masa. Esta gran coincidencia constituye uno de las principios fundamentales de la física, el Principio de Equivalencia, que establece la igualdad entre masa gravitacional y masa inercial:
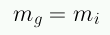
Gracias al Principio de Equivalencia Einstein se dio cuenta que un observador en una caja sin ventanas (ascensor) no podría distinguir si los objetos caen debido a una fuerza gravitacional o si su ascensor está siendo acelerado hacia arriba en el espacio vacío El Principio de Equivalencia implica que un campo gravitacional uniforme es equivalente a un sistema con aceleración uniforme en ausencia de gravedad (esto solo es posible porque todos los cuerpos caen con la misma aceleracion en un campo gravitacional).
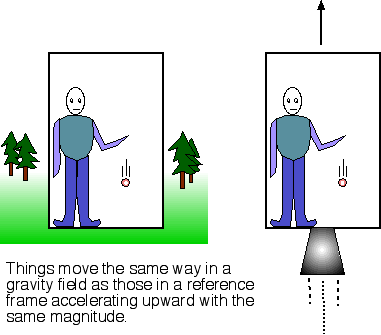
Consecuencias del PE:
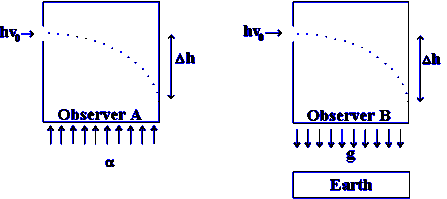
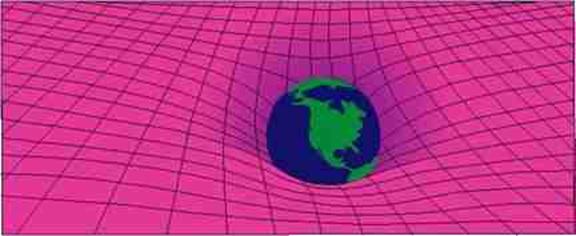

Confirmaciones observacionales de la la deflexión de la luz:

Galaxias distorsionadas por cúmulo Abell 2218

Múltiples imágenes de un cuasar debido a lente gravitacional
Newton no explica como se transmite la fuerza gravitacional. Para Einsten los efectos gravitacionales se manifiestan por medio de la curvatura del espacio. Como la curvatura espacial es independiente de las propiedades de los objetos, resulta natural que la aceleracion sea la misma para todos los objetos y que la masa gravitacional sea equivalente a la masa inercial.
En RG necesitamos poder describir matemáticamente la curvatura del espacio-tiempo. Para esto usamos el concepto de métrica que corresponde a la distancia física entre dos puntos separados por cambios infinitesimales de coordenadas.
El experimento de Michelson-Morley mostró que la velocidad de la luz es independiente del movimiento entre la fuente de luz y el observador. Este es uno de los principios fundamentales de la teoría de la Relatividad Especial (1905).
Si se emite una señal luminosa desde el origen de un sistema de referencia cartesiano S, la ecuación del frente de la onda esférica es c2t2=x2+y2+z2. En un sistema inercial móvil S' que coincide con S en el instante de la emisión la ecuación del frente de la onda esférica es c2t'2=x'2+y'2+z'2 (c=c'). Esta condición determina la transformación de coordenadas entre S y S', la que se denomina "Transformación de Lorentz":
y' = y
z' = z
t' = γ (t - (v/c2) x)
La Relatividad Especial nos enseña que ds2 es la distancia entre dos eventos en un espacio de coordenadas cuadrimensional: el espacio-tiempo.
Entre el observador y una galaxia, dθ = dφ = 0, por lo que
La distancia propia es aquella medida al mismo tiempo -> dt=0. Es una distancia ficticia ya que el Universo se expande y necesitariamos infinitos observadores a lo largo del camino, midiendo los elementos de distancia al mismo tiempo.
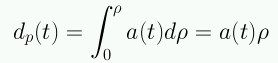
La distancia propia a un objeto con coordenada móvil ρ en el instante actual es:
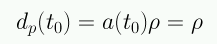
A partir de la distancia propia podemos calcular una velocidad:
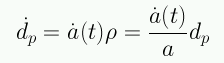
con lo cual recuperamos la ley de Hubble
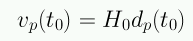
La constante de Hubble corresponde a:
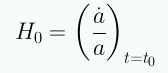
En general:
La constante de Hubble mide la tasa de expansión del Universo en el instante t y cambia en el tiempo. Notar que se puede definir la distancia de Hubble:
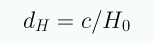
que corresponde a la distancia propia de una galaxia que se aleja actualmente a la velocidad de la luz. Para H0=70 la distancia de Hubble es 4300 Mpc. Las galaxias a distancias propias mayores se mueven a v > c!!! La velocidad se debe a la expansión del espacio y no al movimiento relativo de dos objetos en un espacio estático!
El objeto más lejano que podemos observar (en teoría) es aquel cuya luz fue emitida en te=0 y que nos está llegando en t0. La distancia propia de ese objeto se denomina horizonte .
Dado que los fotones entre el observador y una galaxia se mueven a lo largo de trayectorias con dθ = dφ = 0 y ds2=0,
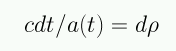
La distancia propia al horizonte se puede expresar como:
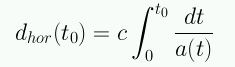
El horizonte es una superficie esférica centrada en el observador, más allá de la cual no podemos ver porque la luz no ha tenido el tiempo de llegar al observador. El horizonte divide el universo visible del universo invisible.

Los fotones entre el observador y una galaxia se mueven a lo largo de trayectorias con dθ = dφ = 0 y ds2=0
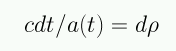
Para un fotón emitido en te y recibido en t0:
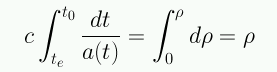
Para un fotón emitido en te+dte y recibido en t0+dt0:
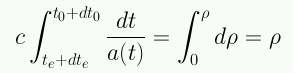
por lo cual,
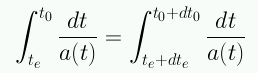
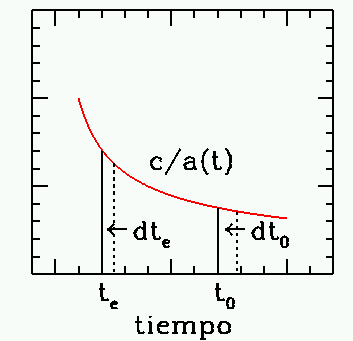
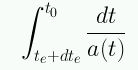
Obtenemos:
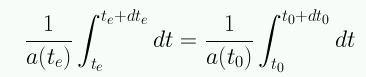
Se ha hecho uso de que a(t) no cambia durante los intervalos dte y dt0. De este modo:
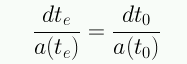
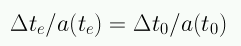
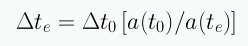
Esta relación se conoce como la dilatación del tiempo. Este efecto ha sido medido experimentalmente a partir de curvas de luz de supernovas.
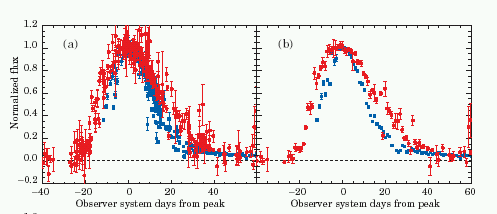
En azul se muestran supernovas a z~0 y en rojo supernovas a z~0.5
Para las ondas de luz, el período de la onda también se dilata. Considerando el período de la onda emitida Δt0 = λ0/c y el de la onda recibida Δte = λe/c
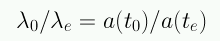
Esta cantidad está relacionada con una cantidad observada:
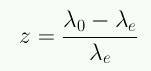
con lo cual