Lectura Obligatoria pregrado: Barbara Ryden (Capítulo 4)
Lectura Sugerida: Carroll (Spacetime & Geometry, secciones 1.1 a 1.10 para una introducción a tensores)
-
Necesitamos conocer k, R0 y a(t). La ecuación de campo de Einstein proporciona
una relación entre la métrica y la distribución de masa-energía. La ecuación de Einstein (1916) es
análoga a la ecuación de Poisson:
- El campo gravitacional fuera de la esfera es como si toda la masa de la esfera estuviera concentrada en el centro
- El campo gravitacional dentro de una cascara esferica hueca es nulo
- Si U>0 ⇒ da/dt>0 ⇒ da/dt nunca llega a cero. Un universo con (da/dt)(t=t0)>0 siempre se expandirá.
- Si U<0 ⇒ existe amax tal que da/dt=0; amax=√-Ur/GM. En algún momento la expansión se detendrá. Como d2a/dt2 < 0, la expansión se convertirá en contracción.
- Si U=0 ⇒
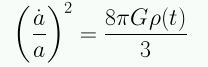
Como M=constante:
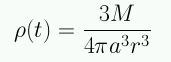
- ε contiene la masa en reposo y el momentum de las partículas
- ε contiene todas las componentes de energía, i.e, ε = ∑ εi (partículas no relativistas, fotones, neutrinos, ondas gravitacionales, y otras formas mas exóticas de energía)
- La energía U corresponde al parámetro de curvatura
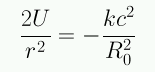
- La ecuación de Friedmann relaciona la curvatura (k y R0), la tasa de expansión a(t), y la densidad de energía ε
- Si Ω < 1 en algún momento, Ω < 1 en todo momento (k=-1)
- Si Ω = 1 en algún momento, Ω = 1 en todo momento (k= 0)
- Si Ω > 1 en algún momento, Ω > 1 en todo momento (k=+1)
- Si ε > 0, aporta aceleración negativa
- La presión tambien aporta a la (des)aceleración (a pesar de no haber gradientes de presión en un universo homogéneo y desafiando nuestra intuición!)
- Una componente de energía con P>0 aporta a la desaceleración, desafiando aún más nuestra intuición!!
- Una componente de energía P < -ε/3 producirá aceleración positiva,
lo que es menos intuitivo aún!!!
IV. La ecuación de estado Hasta ahora tenemos dos ecuaciones: la ecuación de Friedmann y la ecuación de aceleración (a menudo a las dos se les denomina las ecuaciones de Friedmann porque ambas las dedujo él a partir de la ecuación de Einstein).
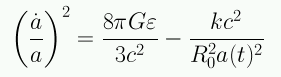
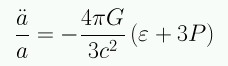
Ahora tenemos 3 incógnitas: a(t), ε(t), P(t) pero sólo dos ecuaciones. La ecuación de estado que relaciona presión y energía, P=P(ε), es la tercera ecuación que permite resolver el problema. Para los casos de interés cosmológico la ecuación de estado se escribe de manera simple:
Para un gas ideal no relativista:
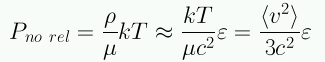
Para un gas de fotones:
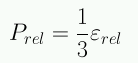
Para la constante cosmológica:
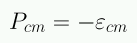
Componentes de energía oscura son todas aquellas que producen aceleración positiva, i.e,
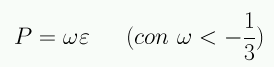
Componentes con ω<-1 u ω>1, no están permitidas porque la velocidad del sonido excedería la velocidad de la luz.
V. La constante cosmológica A partir de 1915 Einstein intentó aplicar la ecuación de campo al Universo real. El se dió cuenta que la principal contribución a la energía viene de la materia no relativista y que la radiación tiene una contribución despreciable. En esa época no existía evidencia de la expansión del Universo (descubierta en 1929) por lo que Einstein creía que el Universo era estático. Sin embargo, las ecuaciones de la Relatividad General no permiten una solución estática usando sólo la componente de energía de materia no relativista. Basta mirar la ecuación de aceleración:
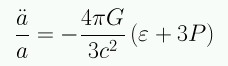
Para un universo cuya principal componente de energía es la materia no relativista tenemos ε > 0 y P=0, por lo cual la aceleración es negativa. El único universo permitido es uno en contracción o expansión.
Einstein resolvió el problema introduciendo a mano un término extra a la ecuación de campo: la constante cosmológica Λ .
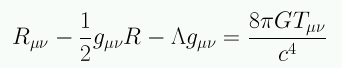
Al incluir Λ, la ecuación de Friedmann queda:
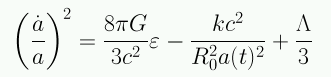
La ecuación de fluido no cambia:
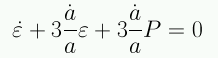
La ecuación de aceleración queda:
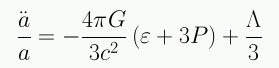
La constante cosmológica juega el rol de una fuerza repulsiva que se opone a la gravedad.
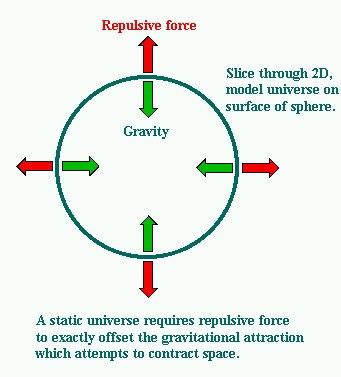
Al mirar las ecuaciones de Friedmann y de aceleración se puede ver que el término Λ equivale a agregar una nueva componente de energía cuya densidad es:
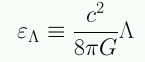
En el caso de una constante cosmológica independiente del tiempo la ecuación de fluído dice que la constante cosmológica tiene asociada una presión negativa:
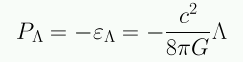
En el caso de la constante cosmológica w=-1, i.e., esta componente constituye un tipo particular de energía oscura.
Una componente con densidad de energía constante tiene asociada una presión negativa y está formalmente de acuerdo con la conservación de la energía (primera ley de la termodinámica).
Cual es el siginficado fisico de la constante cosmologica?
-
Como la constante cosmológica tiene una densidad de energía constante,
cada elemento nuevo de volumen trae asociada su propia energía, por lo
cual esta componente se atribuye a una propiedad
del espacio vacío de origen desconocido, posiblemente de origen
cuántico.
De acuerdo a la física cuántica el principio de incertidumbre permite la constante
creación y aniquilación de pares de partículas y antipartículas en el espacio
vacío. En este marco hay una densidad de energía asociada al vacío de origen
cuántico que es independiente del tiempo a medida que el Universo se expande.
El problema es que no hay una teoría que prediga el valor de esta energía.
Las mejores estimaciones de la energia del vacio debido a fluctuaciones cuanticas
exceden en 122 ordenes de magnitud el valor observado!
-
Otra alternativa es que la constante cosmologica sea una propiedad del espacio-tiempo que aun no entendemos.
- Otra alternativa es que la constante cosmologica sea una constante universal (como la constante de gravitacion) sin explicacion fisica.
Al introducir Λ, Einstein logró obtener el universo estático que él quería (a'=a"=0). La ecuación de aceleración requiere un valor específico de Λ :
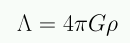
La ecuación de Friedmann muestra que el modelo estático tiene curvatura positiva (k=+1) con un radio de curvatura:
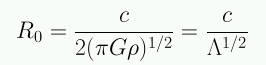
Eintein se dio cuenta que, si bien el modelo era estático gracias al equilibrio entre la gravedad y la constante cosmológica, este universo era inestable.
Notas de interés histórico:
Friedmann se dedicó a descubrir tantas soluciones como fuera posible a las ecuaciones de campo. En particular descubrió que si dejaba a un lado la constante cosmológica, todos los resultados eran universos en expansión llenos de materia. El trabajo de Friedmann, On the curvature of Space, se publicó en un conocido y muy leído periódico alemán de física conocido como Zeitschrift für Physik, el 29 de junio de 1922. Einstein supo del ensayo, no estuvo de acuerdo con los resultados, y rápidamente publicó otro ensayo con su refutación en el mismo Zeitschrift für Physik. Un año más tarde, sin embargo, había reconsiderado su postura. Las soluciones de Friedmann a las ecuaciones de campo eran matemáticamente correctas, admitió Einstein. Sin embargo, le parecía que estas soluciones no tenían validez física: Para producir un universo curvo con las características aparentemente estáticas observadas por los astrónomos se seguía necesitando algo parecido a la constante cosmológica. Ni Einstein ni Friedmann intentaron resolver sus diferencias filosóficas.
En 1927, Georges Lemaître publicó un informe en el que resolvió las ecuaciones de Einstein sobre el Universo entero (que Alexander Friedman ya había resuelto sin saberlo Lemaître) y sugirió que el Universo se está expandiendo, según una de las soluciones, y que es por ello que Slipher y Wirtz habían observado un corrimiento hacia el rojo de la luz de las nebulosas espirales. Sin embargo, aunque ese artículo era correcto y estaba de acuerdo con los datos obtenidos en aquellos años, no tuvo por el momento ningún impacto especial, a pesar de que Lemaître fue a hablar de ese tema, personalmente, con Einstein en 1927 durante un congreso científico sobre física cuántica en Bruselas. Lemaître buscó hablar con Einstein sobre su artículo, y lo consiguió. Pero Einstein le dijo: «He leído su artículo. Sus cálculos son correctos, pero su física es abominable». Lemaître, convencido de que Einstein se equivocaba esta vez, buscó prolongar la conversación, y también lo consiguió. El profesor Piccard, que acompañaba a Einstein para mostrarle su laboratorio en la Universidad, invitó a Lemaître a subir al taxi con ellos. Una vez en el coche, Lemaître aludió a la velocidad de las nebulosas, tema que en aquellos momentos era objeto de importantes resultados que Lemaître conocía muy bien y que se encuentra muy relacionado con la expansión del universo. Pero la situación se volvió bastante embarazosa, porque Einstein no parecía estar al corriente de esos resultados. Piccard decidió huir hacia adelante: para salvar la situación, ¡comenzó a hablar con Einstein en alemán, idioma que Lemaître no entendía!
Cuando Einstein se enteró en 1929 del descubrimiento de Hubble de la expansión del Universo, admitió que la constante cosmológica habia sido la mayor metida de pata de su vida!


Einstein y Hubble en 1931 en la biblioteca de Carnegie Observatories en PasadenaEl gran intercesor de Lemaître fue Eddington. El 10 de enero de 1930 tuvo lugar en Londres una reunión de la Real Sociedad Astronómica. Leyendo el informe que se publicó sobre esa reunión, Lemaître advirtió que tanto de Sitter como Eddington estaban insatisfechos con el universo estático de Einstein y buscaban otra solución. ¡Una solución que él ya había publicado en 1927! Escribió a Eddington recordándole ese trabajo de 1927. A Eddington, como a Einstein y por motivos semejantes, tampoco le hacía gracia un universo en expansión; pero esta vez se rindió ante los argumentos y se dispuso a reparar el desaguisado. El 10 de mayo de 1930 dió una conferencia ante la Sociedad Real sobre ese problema, y en ella informó sobre el trabajo de Lemaître. El 19 de mayo, de Sitter reconoció también el valor del trabajo de Lemaître que fue publicado, traducido al inglés, por la Real Sociedad Astronómica. En 1931, Lemaître propuso la idea que el universo se originó en la explosión de un "átomo primigenio" o "huevo cósmico" (ver artículo). Dicha explosión ahora se llama Big Bang, aunque este nombre fue acuñado recién en 1950 por uno de los detractores de dicho modelo, el astrofísico inglés Fred Hoyle, para mofarse de esta idea.
Había Einstein metido la pata realmente?
mhamuy@das.uchile.cl -
Como la constante cosmológica tiene una densidad de energía constante,
cada elemento nuevo de volumen trae asociada su propia energía, por lo
cual esta componente se atribuye a una propiedad
del espacio vacío de origen desconocido, posiblemente de origen
cuántico.
De acuerdo a la física cuántica el principio de incertidumbre permite la constante
creación y aniquilación de pares de partículas y antipartículas en el espacio
vacío. En este marco hay una densidad de energía asociada al vacío de origen
cuántico que es independiente del tiempo a medida que el Universo se expande.
El problema es que no hay una teoría que prediga el valor de esta energía.
Las mejores estimaciones de la energia del vacio debido a fluctuaciones cuanticas
exceden en 122 ordenes de magnitud el valor observado!
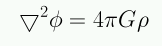
y se escribe:
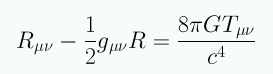

Tμν: tensor energía-momentum describe la distribución de materia y energía
gμν: tensor métrico describe la geometria
Rμν: tensor de Ricci (segundas derivadas de la métrica)
R: escalar de Ricci (segundas derivadas de la métrica)
El lado izquierdo de la ecuación de campo contiene información sobre la curvatura del espacio-tiempo y el lado derecho contiene información sobre la masa y la energía. La ecuación de Eintein relaciona estas dos cantidades y nos dice como responde la curvatura del espacio-tiempo a la presencia de masa y energía.
En el caso de la métrica de R-W, la ecuación de campo da la relación entre a(t), k, R0 y la distribución de masa-energía. Esta ecuación lleva el nombre del matemático y meteorólogo ruso Alexander Friedmann (1888-1925; ver biografía) quien la dedujo en 1922. El sacerdote belga Georges Lemaître (1894-1966; ver biografía) obtuvo independientemente soluciones a la ecuación de campo en 1927.

Isaac Newton (1642-1727)
Supongamos un universo homogéneo, isotrópico e infinito, consideremos una esfera dentro del Universo, y estudiemos el movimiento de una partícula de masa m sobre la superficie de la esfera.
Teoremas esféricos de Newton (1642-1727; ver biografía):
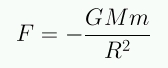
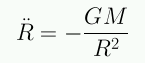
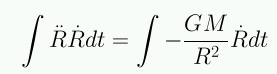

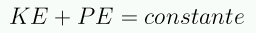
La masa dentro de la esfera es constante:

Para expansión isotrópica R(t) = a(t)r (r: radio comóvil).
Ecuación de Friedmann en forma Newtoniana:
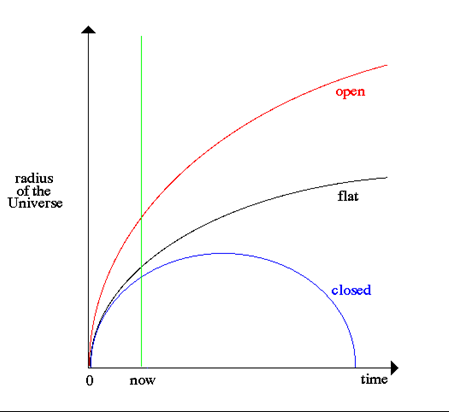
Esta ecuación admite 3 tipos de soluciones:
Los 3 destinos posibles de la esfera en un Universo newtoniano son análogos a la suerte de una piedra lanzada hacia arriba.
Usando la ecuación de campo de Einstein y la métrica de R-W se llega a la ecuación de Friedmann:

Alexander Friedmann (1888-1925)
Usando la definición de la constante de Hubble, H(t)=a'/a, la ecuación de Friedmann queda:
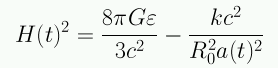
Para un universo plano (k=0):
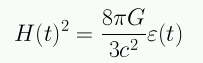
Dado H(t) hay una densidad crítica:
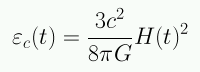
En el instante actual:
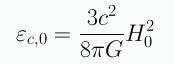
Para H0=70 la densidad de energía crítica actual es de 8.3 × 10-10 J m-3, o bien, 5200 MeV m-3. Su equivalente en masa crítica se obtiene dividiendo por c2: 9 x 10-27 kg m-3 (el equivalente a 6 protones m-3). Mientras mayor sea H0, mayor es la densidad crítica: se necesita mas energía para frenar la expansión.
En la discusiones de curvatura habitualmente se usa el parámetro de densidad (adimensional):
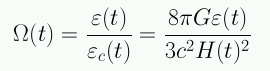
En términos del parámetro de densidad la ecuación de Friedmann se escribe:
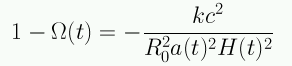
Como el signo del lado derecho no cambia a medida que el Universo se expande:
En el momento actual
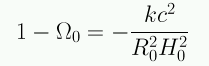
Si se conoce Ω0, podemos conocer el parámetro de curvatura.
Si además se conoce H0, podemos calcular el radio de curvatura R0.
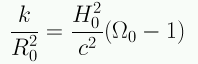
La ecuación de Friedmann involucra dos incógnitas: a(t) y ε(t), por lo cual es necesaria una ecuación adicional. El Universo debe satisfacer la primera ley de la termodinámica:
Para un universo homogéneo entonces cualquier elemento de volumen debe satisfacer dQ=0, por lo cual
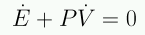
Consideremos una esfera de radio a(t)r, el volumen es
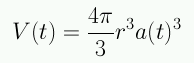
y la derivada del volumen es
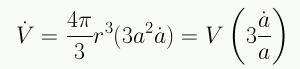
La energía interna de la esfera es
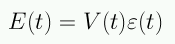
y la derivada es
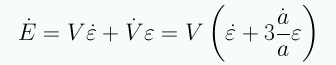
En un universo en expansión la 1a ley de la termodinámica toma la forma:
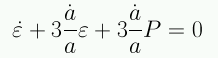
Esta es la ecuación de fluído .
Usando la ecuación de Friedmann y la ecuación de fluído obtenemos la ecuación de aceleración :