Lectura Obligatoria: Barbara Ryden (Capítulo 5)
Lectura Sugerida:
-
Tenemos 3 ecuaciones independientes para la dinámica del Universo y 3 incógnitas: ε(t), P(t) y a(t):
- Partículas relativistas (radiación):



La densidad de radiación decae más rapido que la densidad de la materia!
- Densidad de radiación asociada al CMB actualmente es:
εCMB,0 = α T4 = 7.56 × 10-16 × 2.734 = 4.17 × 10-14 J m-3 y el parámetro de densidad es:ΩCMB,0 = εCMB,0 / εc,0 = 4.17 × 10-14 / 8.3 × 10-10 = 5 × 10-5 Esta componente no juega un papel importante en la expansión actual, pero sí jugó un papel importante en las etapas tempranas del Universo.
- La densidad de radiación asociada a las estrellas es mucho menor:
εestrellas,0~1 × 10-15 J m-3 y esta componente se puede ignorar ahora y siempre.
- Densidad de energía asociada a los neutrinos.
En teoría se espera que exista un Fondo Cósmico de Neutrinos (CNB) análogo al CMB. Asumiendo
que los neutrinos se comportan de manera relativista se espera εν,0 = 0.681 × εCMB,0.
Los neutrinos cósmicos aún no se han detectado. Si efectivamente existe el CNB su parámetro de densidad sería:
Ων,0 = 0.681 × ΩCMB,0 = 3.4 × 10-5
- Densidad de radiación asociada al CMB actualmente es:
- Materia no relativista:



Las mediciones actuales favorecen un universo con
Ωm,0 = 0.3 La densidad de energía de materia no relativista es sólo un 30% de la densidad crítica. - Constante cosmológica:


Las mediciones actuales favorecen un universo con
ΩΛ,0 = 0.7 - La densidad de energía asociada a la constante cosmológica es la componente dominante
en la actualidad. Sin embargo,

Para a=0.75 el Universo tenía igual contribución energética de la materia y la constante cosmológica. Esto corresponde a z=0.33. Antes de esto la materia dominaba sobre Λ.
- La densidad de energía de radiación es la menos importante hoy día. Sin embargo,

Para a=1/3600 (z~3600) la componente de radiación era igual a la componente de materia. A redshifts mayores se habla de la era de radiación porque esta era la componente dominante. Esta era fue seguida por una era de la materia, y hoy día vivimos en la era de la constante cosmológica.
- k=+1 está prohibido porque a' sería imaginario
- k=0 está permitido ya que a'=0 ⇒ a(t)=constante
Universo vacío, plano y estático (descrito por la métrica de Minkowski) - k=-1:
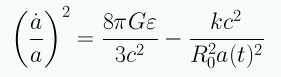
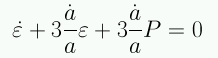
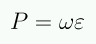
La solución para a(t) se complica debido que el Universo contiene diferentes componentes de energía. Al menos hay dos componentes obvias: materia no relativista y radiación. En los ultimos años ha aparecido evidencia observacional de que hay otras formas de energía más exóticas. Afortunadamente la solución a las ecuaciones anteriores se simplifica gracias a que tanto la densidad de energía como la presión de las distintas componentes son cantidades aditivas, i.e,


La ecuación de fluido se debe satisfacer para cada componente individual:


Asumiendo que ωi es independiente del tiempo:

Veamos algunos ejemplos de componentes:

Evolución de las tres componentes principales de energía

Este es un Universo vacío sin radiación, sin materia, sin constante cosmológica ni energía de ningún tipo. En este caso:




t0 es la edad del Universo.

Usando la definición de la constante de Hubble:

Si medimos H0 podemos saber el radio de curvatura actual del Universo.
Al no haber atracción gravitacional el Universo se expande sin desaceleración, i.e., a"=0.
Redshift:

Si medimos el redshift podemos saber en que instante fue emitida la luz:

Para z=0, te=t0 mientras que para z=∞, te=0.
Para la métrica de R-W, la distancia propia se expresa en general:


Al medir z podemos saber la distancia propia al objeto. A redshifts pequeños la relación entre d y z es lineal (ley de Hubble). Si z=0 → d=0.


Un universo plano sólo con materia se denomina Einstein-de Sitter. La ecuación de Friedmann para w=0 se reduce a:

La solución para este caso es:




Notar que la edad del Universo es menor que el tiempo de Hubble.
Redshift:

Distancia propia:


La distancia al horizonte es mayor que la distancia de Hubble:

En un universo plano dominado por materia un observador sólo puede ver una parte del Universo. Nada fuera del Universo visible tiene influencia sobre el observador.
Este es un caso especial del modelo plano. Este es un buen modelo para las épocas tempranas del Universo en donde dominaba la radiación. La ecuación de Friedmann para w=1/3 es:

La solución para este caso (ω=1/3) es:





Evolución de la densidad de energía y la temperatura:


En un universo plano dominado por radiación (ω=1/3), un observador sólo puede ver una parte del Universo. Nada fuera del Universo visible tiene influencia sobre el observador.
Ahora consideremos un universo plano con ω=-1. La ecuación de Friedmann toma la forma:


El Universo se expande exponencialmente y es infinitamente viejo. El redshift permite calcular el instante de la emisión:

y también permite calcular la distancia propia a la fuente:

La distancia propia varía linealmente con z (lo cual no era cierto para los otros modelos).
En un universo plano con ω=-1 el horizonte es infinito y todo el Universo está en contacto causal con el observador.


mhamuy@das.uchile.cl