Lectura Obligatoria: Barbara Ryden (Capítulo 7: Sec 7.1, 7.2)
Lectura Sugerida:
-
Si conociéramos la densidad εi para cada componente de energía podríamos usar la
ecuación de Friedmann para determinar la historia de la expansión cósmica a(t). A la inversa, si pudiéramos medir
el factor de escala a(t) a partir de las observaciones podríamos usar esa informacion para determinar εi
para cada componente del Universo. Este es uno de los propósitos más importantes de la cosmología. El problema es
que el factor de escala no se puede observar directamente. Podemos obviar este problema midiendo cantidades
observables tales como redshift, distancias, tamaños angulares que sí dependen de los parámetros εi.
Es imposible medir como varía el factor de escala a(t) desde el Big Bang, pero sí podemos hacer mediciones que nos permiten determinar a(t) para épocas cercanas a t0. Para esto podemos efectuar una expansión de Taylor cerca de t0 para las cantidades de interés:

Dividiendo por a(t0):

Usando la definición de la constante de Hubble H(t) y del parámetro de desaceleración q(t):

la ecuación para a(t) queda:

Notar que el parámetro q es adimensional y es negativo cuando el Universo se desacelera y es positivo cuando se acelera. En esta expansión de Taylor los parámetros H y q describen la cinemática. Podemos usar la ecuación de la aceleración:

para ver como depende q de los parámetros cosmológicos. Recordando la definición de densidad crítica y parámetro de densidad:

la ecuación de aceleración da una relación entre q y los parámetros de densidad de las distintas componentes del Universo:

Para un universo sólo con radiación, materia común y constante cosmológica:

Podemos ver que si logramos medir q0 podemos determinar una combinación de parámetros εi. Los valores individuales no pueden deducirse a partir de q0. Esto es lo que se llama "degeneración". Para remover la degeneración se requieren mediciones adicionales. Usando los valores del modelo benchmark ΩΛ,0=0.7, Ωm,0=0.3 y Ωr,0≈0 obtenemos q0=-0.55. Durante la expansión el parámetro de aceleración muestra la siguiente evolución:

Este gráfico muestra claramente las tres eras del Universo y los valores esperados para cada una de ellas (1 para la era de radiación, 0.5 para la era de la materia, y -1 para la era de la constante cosmológica).
Una cantidad que es fácil de medir es el redshift, el cual contiene informacion sobre el factor de escala en el momento de la emisión. Por definición:

Usando la expansión de Taylor para a(t) se puede demostrar que:

El redshift nos da informacion sobre el "look-back time", i.e., el tiempo de viaje de los fotones entre la fuente y el observador.
Invirtiendo la ecuación anterior obtenemos una aproximacion para el look-back time a partir del redshift:

La relación es lineal para redshifts pequeños.
La distancia propia no se puede medir directamente pero veremos que podemos medir ciertas cantidades estrechamente ligadas a la distancia propia. Por definición la distancia propia está ligada al factor de escala:

Usando la expansión para a(t) podemos obtener la siguiente aproximación para la distancia propia a partir del look-back time:

El primer término corresponde a la distancia en un universo plano y estático. El segundo término es una corrección debido a la expansión. Usando la relación anterior entre look-back time y redshift obtenemos una relación aproximada entre distancia propia y redshift:

A redshifts pequeños se obtiene la habitual ley de Hubble en que dp∝z. Esta linealidad es válida para todo z sólo en el caso qo=-1. En general se espera observar una curvatura en el diagrama de Hubble a redshifts altos, la cual está determinada por qo.
La distancia lumínica se define usando la ley del inverso del cuadrado:
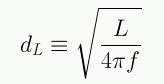
En el capitulo 2 (Sec. VII) vimos que en la aproximación de un universo plano la relación con la distancia propia es:
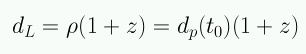
En el límite de bajos redshifts la expansión de Taylor arroja:


Para un cambio δq0, el cambio esperado en la distancia es:

Por ejemplo, para distinguir entre modelos que difieren en δq0=0.5 a z=0.5 necesitamos medir distancias con precisiones de 12.5%. A redshifts más altos no se requiere tanta precisión pero los objetos son más débiles y difíciles de observar.
Para un cambio δq0, el cambio esperado en magnitud es:

Para distinguir entre modelos que difieren en δq0=0.5, a z=0.5 necesitamos medir magnitudes de patrones lumínicos con precisiones de 0.27 mag.
mhamuy@das.uchile.cl