Lectura Obligatoria Posgrado: Freedman et al. (2001, ApJ, 553, 47)
Lectura Sugerida: Sandage et al. (2006, astro-ph/0603647)

Capítulo 7: Determinación de distancias extragalácticas

Las distancias son imprescindibles para:
• Determinar propiedades intrínsecas de las galaxias: diámetros, luminosidades,...
• Hacer mapas de la distribución de las galaxias
• Estudiar la expansión del Universo: edad, evolución, y su destino
I. Métodos genéricos
• La paralaje trigonométrica no sirve para objetos extragalácticos

• Tamaños angulares: si conocemos el tamaño físico de un objeto podemos determinar su distancia (d = r/θ)

• Patrones lumínicos: si conocemos la luminosidad de un objeto podemos determinar du distancia lumínica usando la ley del inverso del cuadrado:
  

• Ley de Hubble:
  
  II. Método de las estrellas Cefeidas

• Las Cefeidas son estrellas muy luminosas (10²-10⁵ L_sol) y de luminosidad variable

  

• Mientras examinaba estrellas variables en la Nube Chica de Magallanes, Henrietta Leavitt descubrió en 1907 la relación periodo-luminosidad:
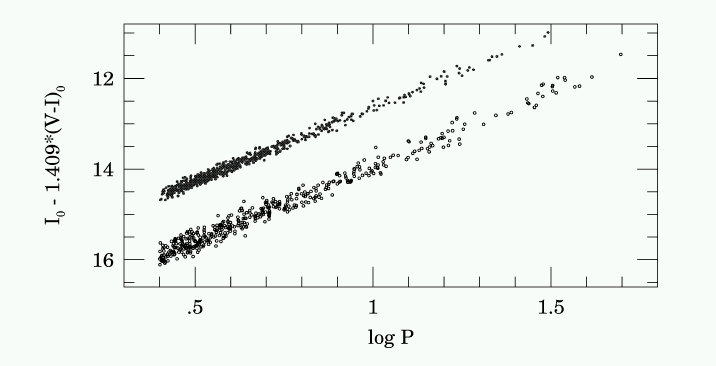
  Relación periodo-luminosidad según proyecto OGLE (Udalski et al. 1999) para LMC y SMC

• Si descubrimos Cefeida(s) en otra galaxia NGC y medimos su(s) periodo(s) podemos usar la ley del inverso del cuadrado para determinar distancias relativas:
  
• La relación periodo-luminosidad tiene una dispersión de sólo 0.16 mag en el filtro V, i.e., 16% en flujo ⇒ solo 8% en distancia

• Pero cual es la distancia absoluta?
  Necesitamos la distancia a la LMC. Como se mide esta distancia?
  III. La distancia a la Nube Grande de Magallanes

• Paralaje a δ Cep con el HST da distancia de 273 ± 11 pc :
  

  Si adoptamos V=3.71 obtenemos M_V=-3.47 para δ Cep. Una Cefeida del mismo periodo en la LMC (log(P)=0.73) tiene V=15.03, por lo cual el módulo de distancia a la LMC es 18.50.

• Paralaje a RR Lyrae con el HST da distancia de 262 ± 14 pc: Si adoptamos una magnitud aparente V=7.70 obtenemos una magnitud absoluta de M_V=+0.61. Usando la magnitud aparente de estrellas RR Lyrae en la LMC se deduce un módulo de distancia de 18.38-18.53.

• Medición del tamaño físico y angular del anillo de la SN 1987A :

  Ref: Panagia et al. (1991, ApJ, 380, L23), Gould et al. (1994, ApJ, 425, 51)

  
  (después) Supernova 1987A (antes)
  
  La Nube Grande Magallanes (izquierda) y la nebulosa Tarántula junto a SN 1987A (derecha)
  • La supernova 1987A explotó el 24 de febrero de 1987. 83 días después de la explosión, el satelite IUE detectó líneas de emisión delgadas de He, O, N y C. El flujo de las líneas aumentó alcanzando un máximo 413 días después de la explosión. Esta observación fue interpretada como emisión de material circum-estelar ionizado por la radiación de la supernova.

  • Un año mas tarde, cuando la supernova se había se habia debilitado, se obtuvo evidencia directa de la presencia de este material a partir de imágenes directas.
    
    El anillo de la SN 1987A (Feb 1996)

  • Observaciones posteriores revelaron que la geometría del material circum-estelar era la de un anillo circular inclinado en 43⁰ y centrado en la supernova. La inclinación c/r a la línea de visión hace que el anillo aparezca como una elipse en el plano del cielo con un eje mayor de 1.7" y eje menor de 1.2".

  • Medición de la distancia:
    • El diámetro físico del anillo se pudo determinar a partir del tiempo de viaje entre la luz emitida desde el punto más cercano y el más lejano del anillo
      Para Δt = 330 días ⇒ 2a= 1.27 × 10¹⁸ cm

    • El diámetro angular se pudo medir de manera precisa con imágenes del telescopio espacial ⇒ 1.66"
    • Distancia = 1.27 × 10¹⁸ × 206265 / 1.66 = 1.58 × 10²³ cm = 51 ± 3 kpc lo que equivale a un módulo de distancia de 18.55.

  Distancia a la Nube Grande de Magallanes

  Técnica	Módulo de Distancia	Referencia
  Cefeidas (δ Cep)	18.50 ± 0.13	Benedict et al. (2002, AJ, 124, 1695)
  R Lyrae	18.38-18.53	Benedict et al. (2002 AJ, 123, 473)
  Anillo SN 1987A	18.55 ± 0.12	Panagia et al. (1991, ApJ, 380, L23)

• Hay muchos otros métodos...
  
  IV. Aplicación del método de Cefeidas a galaxias más lejanas

  Uno de los objetivos principales del telescopio espacial (HST) ha sido la determinación precisa de la constante de Hubble. Dos equipos independientes de astrónomos dirigidos por Allan Sandage y Wendy Freedman usaron el HST para descubrir Cefeidas en galaxias lo más lejanas posible.

• Freedman et al. (2001, ApJ, 553, 47) descubrieron Cefeidas en 18 galaxias espirales entre 1-22 Mpc. Adoptando una relación periodo-luminosidad basada en una distancia de 50 kpc para la LMC,
  

  obtuvieron el siguiente diagrama de Hubble:

  

  El valor de H₀ que mejor se ajusta a los datos es 75 ± 10.

  Este diagrama revela errores pequeños en las distancias, pero errores muy grandes en los redshifts. Esto se debe a que los movimientos aleatorios de las galaxias afectan significativamente los redshifts cosmológicos. Para resolver este problema se necesitan distancias a galaxias más lejanas. Debido a su enorme luminosidad (10⁷-10⁹ L_sol) las supernovas de tipo Ia son los objetos astrofísicos preferidos para este propósito.

  Freedman et al. usaron distancias Cefeidas a 7 galaxias que habían albergado supernovas de tipo Ia en el pasado, para calibrar las luminosidades de las supernovas. Esta calibración fue usada para determinar distancias a ~30 supernovas lejanas del proyecto Calán/Tololo (con redshifts entre 0.01-0.1), lo cual arrojó una constante de Hubble de 71 ± 6.

• Sandage et al. (2006, astro-ph/0603647) usaron el HST por 15 años el HST para descubrir Cefeidas en 10 galaxias que habían albergado supernovas de tipo Ia en el pasado con el fin de calibrar las luminosidades de las supernovas

  Las 7 galaxias en común con la muestra de Freedman resultan tener distancias sistemáticamente (10%) mayores, lo cual se traduce en una disminucion de la constante de Hubble a 62 ± 5

  
  Patente de Allan Sandage en 2001

  Parte de las diferencias se deben a:

  • métodos para calcular los flujos de las Cefeidas (fotometría)
  • métodos para corregir los flujos por la absorción de polvo
  • la relación periodo-luminosidad
  • la distancia a la LMC
  • exceso de pasión!
  La controversia continua!
  
  La constante de Hubble en el tiempo
  V. Determinación de distancias usando supernovas de tipo Ia

  Ref: Hamuy et al. 1996 (AJ, AJ, 112, 2398), Phillips et al. 1999 (AJ, 118, 1766)

  Para obtener una medida precisa de la constante de Hubble es necesario determinar distancias a galaxias con redshifts mayores a 0.01. Las Cefeidas sólo permiten medir distancias hasta 25 Mpc (lo que corresponde a z=0.006).

• Las supernovas de tipo Ia tienen una enorme luminosidad (10⁷-10⁹ L_sol) lo que las convierte en objetos muy atractivos para este fin.
  
  (izq) SN 1994D. (der) Modelo de SN Ia.

• Debido a la ausencia de hidrógeno en el espectro y a la ocurrencia en galaxias sin formación estelar, el modelo estándar es el de la explosión de una enana blanca que acreta masa de una compañera y explota al aproximarse a la masa de Chandrasekhar (1.4 M_sol).

• Las SNs Ia tienen curvas de luz de este tipo:
  SN 1992bc

  y se usa la magnitud en el máximo como estimacion del flujo.

• Al igual que con las Cefeidas podemos intentar usar los flujos de las SNs para medir distancias relativas entre una galaxia X y una galaxia NGC:
  

• Pero, cual es la distancia absoluta?

  Necesitamos la distancia a la galaxia NGC. Como?

• Usando el método de las Cefeidas:
• con lo cual:

• Esto demuestra que el método para objetos mas distantes depende de un método mas cercano, el cual depende de métodos aún más cercanos. Esta cadena de métodos, cada uno dependiendo del anterior, es lo que se denomina ESCALA DE DISTANCIAS EXTRAGALACTICAS, en el sentido que para acceder al nivel más alto es necesario pasar por los niveles (peldaños) más bajos.
• La escala de distancias extragalácticas se afirma en la distancia a la LMC. Cualquier error en esta distancia se propagará hacia los objetos más lejanos.
• El método de las SNs asume que las luminosidades de todos estos objetos son las mismas. Es razonable asumir esto?
• Para investigar esto podemos usar los redshifts de las galaxias huéspedes de las SNs de la muestra Calán/Tololo para llevar todas las SNs a una misma distancia y comparar sus luminosidades:
  

• Podemos calcular el flujo que tendrían las SNs a una distancia fiducial (10 pc):
  

  y la magnitud absoluta:

  
• Curvas de luz absolutas: Esto demuestra que las SNs Ia NO son buenos patrones lumínicos (standard candles)

• Sin embargo, aparece relación empírica entre la luminosidad en el máximo y el ancho de la curva de luz (Peak luminosity-decline rate relation ).
  

  Esta relación permite usar el ancho de la curva de luz para estandarizar las luminosidades de las SNs Ia como si fuera un "dimmer". Las SNs Ia resultan entonces patrones lumínicos estandarizables (standarized candles) tal como las Cefeidas.

• Receta para determinar distancias con SNs Ia:
  • Medir Δm₁₅ a partir de curva de luz de una SN en galaxia X
  • Medir magnitud aparente en el máximo
  • Usar la relación "dimmer" para corregir su magnitud aparente
  • Hacer lo mismo para una SN Ia en una galaxia (NGC) con distancia conocida
  • Usar el cuociente de los flujos corregidos de las dos SNs para determinar la distancia a galaxia NGC

• Precisión del método de las SNs Ia: la relación "dimmer" tiene una dispersión ~0.15 mag en el filtro V, i.e., 15% en flujo ⇒ sólo 7% en distancia (igual que las Cefeidas)

• Diagrama de Hubble
  Diagrama de Hubble con SNs Calán/Tololo. La caja en la esquina izquierda muestra el rango examinado originalmente por Hubble en 1929.

• Constante de Hubble es de 62 ± 5 usando la calibración de Sandage ó 71 ± 6 usando la calibracion de Freedman.
  VI. Determinación de distancias usando supernovas de tipo II

• Las SNs de tipo II ocurren sólo en galaxias con alta formación estelar y muestran espectros ricos en hidrógeno. Se atribuyen a estrellas masivas que nacen con más de 8 M_sol y explotan luego de sufrir el colapso gravitacional de sus núcleos.
  
  SN 1999em
• Las SNs II son 2× más frecuentes que las SNs Ia, pero son menos luminosas (10⁸-10⁶ L_sol).
• La mayoría de las SNs II muestran una curva de luz de tipo "plateau" y un gran rango en luminosidad:
  
• Sin embargo, aparece relación empírica entre la luminosidad medida en el medio del plateu y la velocidad de expansión de la SN medida en el mismo instante (relación luminosidad-velocidad):
  
• Esta relación permite usar velocidades medidas espectroscópicamente para estandarizar las luminosidades de las SNs II. La dispersión en esta relación es ~0.3 mag, lo que permite determinar distancias con una precisión de 15%.
  VII. El método Tully-Fisher para galaxias espirales

  Ref: Giovanelli et al. (1997, AJ, 113, 22), Sakai et al. (2000, ApJ, 529, 698)

• Las galaxias espirales son luminosas, pero muestran un gran rango de luminosidades por lo cual no es posible usarlas como patrones lumínicos.

• Las galaxias espirales rotan:

  A partir del desplazamiento Doppler de las líneas se puede determinar la velocidad de rotación de la galaxia:

  y la curva de rotación :
• Al medir las curvas de rotación de las espirales a partir de la emisión de 21-cm de H neutro, Tully y Fisher encontraron en 1977 que las galaxias más masivas (más luminosas) muestran mayores velocidades rotacionales máximas.
• La relación de T-F es aproximadamente L ~ v_MAX⁴, pero la forma exacta depende del tipo de Hubble.
• Orígen físico de la relación T-F:

  Ley de Newton:

  

  Las galaxias espirales muestran un brillo superficial constante:

  

  De lo cual se desprende la relación T-F:

  
• La relación de T-F permite estandizar las luminosidades de las espirales y usarlas como indicadores de distancias. La dispersión de la relación es 0.35 mag, lo que permite determinar distancias con una precisión de 17%.
  VIII. El método Faber-Jackson para galaxias elípticas

• Las galaxias elípticas son aún más luminosas que las espirales, pero también muestran un gran rango de luminosidades por lo cual no es posible usarlas como patrones lumínicos.

• Las elípticas no muestran mayor grado de rotación, incluso aquellas achatadas. Las estrellas se mueven con velocidades aleatorias cuya dispersión (σ₀) se se puede medir por el ensanchamiento de las líneas espectrales debido al efecto Doppler que afecta a las estrellas individuales.

• En 1976 Faber y Jackson identificaron una correlación entre la dispersión de velocidad central radial y la luminosidad de la galaxias elípticas.

• La relación de F-J tiene la forma L ~ σ₀⁴

• La relación mejora al incluir el radio efectivo de la galaxia: L ~ σ₀^2.65 r_e^0.65 relación conocida como plano fundamental .
  IX. El método de las fluctuaciones de brillo superficial (SBF)

  Ref: Tonry et al. (2000, ApJ, 530, 625)

  Una galaxia está compuesta de estrellas individuales. Cuando observamos con un CCD cada pixel contiene un número finito de estrellas. A medida que una galaxia se aleja del observador más estrellas caen en cada pixel, lo cual disminuye las fluctuaciones de Poisson entre pixel y pixel. Al ir perdiendo resolución espacial las fluctuaciones de brillo superficial disminuyen (viéndose más suave). La magnitud de las fluctuaciones es un buen indicador de distancia para galaxias elípticas con una precision ~15%.

  
  X. El método de la expansión fotoesférica para supernovas de tipo II (EPM)

  Ref: Dessart et al. (2006, A&A, 447, 691)

• Las SNs de tipo II tienen un espectro parecido a una distribución de Planck lo cual permite determinar su radio angular vía:
  

  El parámetro ζ da cuenta de las diferencias del simple modelo de cuerpo negro y viene dado por modelos de atmósferas de SNs de tipo II.

• Las velocidades de expansión de la supernova se pueden medir espectroscópicamente a partir del efecto Doppler, con lo cual podemos obtener el radio físico:
  

• Combinando estas dos ecuaciones podemos escribir la ecuación EPM:
  

  Con dos observaciones obtenidas a distintas épocas podemos encontrar la distancia D y el tiempo de la explosión t₀. Con más de dos épocas obtenemos un valioso test de consistencia interna.

• Este método no requiere una calibración externa, por lo cual es independiente de la escala de distancias extragalácticas!
  XI. Alcance de los métodos para determinar distancias extragalácticas
  
  XII. Corrección K

  Uno de los propósitos de medir distancias es la determinación de los parámetros cosmológicos. Como los modelos cosmológicos se asemejan mucho entre sí a bajo z, para poder discriminar modelos se hace necesario observar objetos a alto z. Una dificultad de medir magnitudes de objetos lejanos es que el espectro se desplaza c/r a z=0, lo que equivale a que la banda instrumental se desplace hacia el azul y que nuestro sistema instrumental cambien según el redshift del objeto. Esto se traduce en que la magnitud observada de un objeto a redshift z sea diferente a aquella que mediríamos si el objeto estuviese a z=0. Esta diferencia de magnitud es lo que se denomina corrección K y se define como:

  

  En esta ecuación N(λ) es el flujo de fotones por unidad de longitud de onda de un objeto a z=0 y S(λ) es la función de transmisión de la banda de paso del filtro utilizado.

  La definición de corrección K tiene dos términos. El primer término da cuenta de que el espectro se estira, lo que equivale a que la banda se angoste en el sistema en reposo del objeto a redshift z. Este termino es independiente de z y de la forma de N(λ). El segundo término es la razón del flujo transmitido por el filtro del espectro desplazado al rojo y la razón del flujo transmitido por el mismo filtro del espectro a z=0. Este término se puede calcular numéricamente para un objeto con espectro conocido.

  Habitualmente esta definición está dada incorrectamente en la literatura con el flujo de energía F(λ) en vez del flujo de fotones N(λ) (ver, por ejemplo, Oke & Sandage 1968, ApJ, 154, 21). La definición correcta debe ser en términos de N(λ) ya que los detectores cuentan fotones y no energía.

  Notar que a corrección K debe considerarse como una corrección instrumental ya que, si el detector fuese un bolómetro sensible a todas las longitudes de onda, la corrección K sería nula.