- 1. De qué está hecho el Universo?
- 2. Es espacialmente finito o infinito?
- 3. Tuvo un comienzo o ha existido por siempre?
- 4. Existirá por siempre o habrá un final?
I. Hechos Observacionales Relevantes La cosmología moderna nace hace apenas 100 años cuando comienzan a obtenerse datos de fuentes externas a la Vía Láctea. Estas observaciones revelan que todo emergió de un punto denso y caliente de energía y materia que comenzó a expandirse hace 13500 millones de años. Este modelo del Big Bang se fundamenta en tres observaciones:
- 1. La ley de expansión de Hubble
- Las galaxias muestran un espectro corrido al rojo según observaciones de Vesto Slipher
entre 1912-1925. Se define el parametro redshift
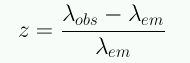

Corrimiento al rojo - En 1925, Edwin Hubble (1889-1953)
logró resolver la nebulosa de Andrómeda en estrellas individuales y descubrir estrellas
variables Cefeidas, demostrando que en realidad esta nebulosa es una galaxia externa
a la Vía Láctea. Al estudiar otras nebulosas Hubble demuestra que Andrómeda no es
una excepción, demostrando así que el Universo es mucho más grande de lo
que se pensaba.
Estrella Cefeida - En 1929, Hubble había logrado identificar Cefeidas en 24 galaxias y determinar sus
distancias. Al combinar sus resultados con aquellos de Slipher, Hubble descubrió que
el redshift es proporcional a la distancia → el Universo se encuentra en expansión!!!
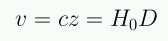
H0 es la famosa constante de Hubble (unidades de km s-1 Mpc-1 y dimensiones de T-1) cuyo valor es entre 60-80.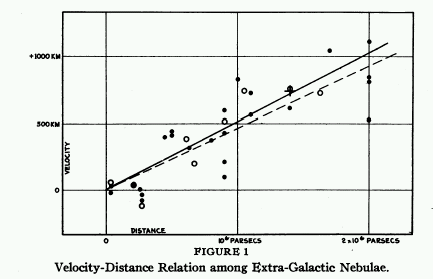

Ley de Hubble - Estamos en el centro de la expansión? No, lo que vemos desde nuestra galaxia
es exactamente lo mismo que vería un observador en cualquier otro lugar
del Universo. Consideremos dos galaxias A y B:
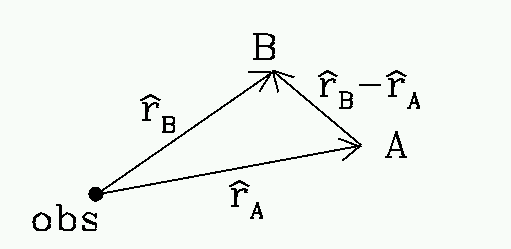
De acuerdo a la ley de Hubble:
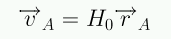
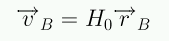
La velocidad de expansión de B con respecto a A es:
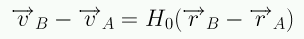
O sea,
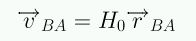
Por lo tanto, un observador en A ve la expansión con la misma ley que un observador en nuestra galaxia → la ley de Hubble satisface el Principio Cosmológico, el cual establece que todos los observadores son iguales y que no hay centro en el Universo.
- La idea de un universo en expansión había sido propuesta usando la teoría de la Relatividad
General (formulada por Einstein en 1916) antes del descubrimiento de Hubble. Tanto el holandés
de Sitter (1917), el ruso Friedmann (1922), como el belga Lemaître (1927) obtuvieron soluciones
de un universo en expansión. Einstein, sin embargo, no estaba al tanto de las observaciones de
Slipher y modificó la teoría de la RG para obtener soluciones estáticas. Einstein
refutó los trabajos de de Sitter, Friedmann y Lemaître hasta la publicación de Hubble en 1929.
En ese momento Einstein tuvo que admitir su error y volver a la forma inicial de la RG.
- La expansión implica que en algún momento en el pasado toda el Universo observable estuvo
concentrado en un pequeño volumen. Esta noción fue introducida en 1927 por el sacerdote belga
Georges Lemaître bajo el nombre de "átomo primitivo", el cual se conoce hoy como BIG BANG.
- Asumiendo una expansión uniforme el tiempo transcurrido desde que las galaxias estaban juntas es 1/H0.
Esta cantidad se denomina el tiempo de Hubble (~14 Gyrs).
- Las galaxias muestran un espectro corrido al rojo según observaciones de Vesto Slipher
entre 1912-1925. Se define el parametro redshift
- 2. La abundancia de elementos químicos primordiales (nucleosíntesis del Big Bang)
- La abundancia de los elementos químicos más livianos (hidrógeno y helio) se puede
explicar debido a la fusión nuclear cuando el Universo era joven, denso y caliente
(animación).
- En los años 1950's la teoría sobre la formación de los elementos de la
Tabla Periódica postulaba que todos los elementos más pesados que el Hidrógeno
se producen en los interiores de las estrellas. Esta teoría predecía que sólo
1-4% de toda la materia del Universo debía estar en forma de Helio. Sin embargo,
el 25% del Universo está en forma de Helio.
- George Gamow y sus colaboradores postularon a fines de los años 40's que
la síntesis de Helio, del Deuterio y del Litio ocurrió en los primeros minutos
luego del Big Bang (a fuego rápido) y que los elementos más pesados que el Litio
se originaron mucho después en los núcleos de las estrellas (a fuego lento).
- En los primeros segundos del Universo las temperaturas alcanzaban cientos de
millones de grados, demasiado caliente para que los núcleos atómicos pudieran
subsistir.
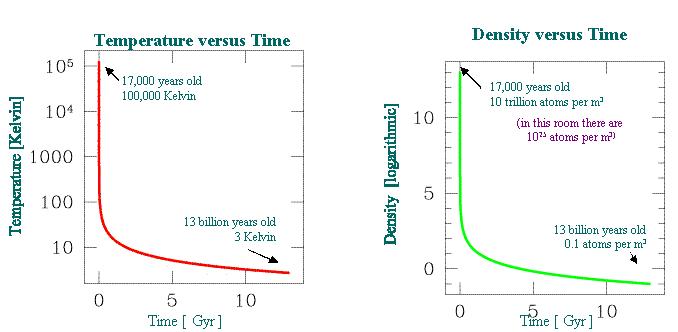
Al cabo de unos 3 minutos la temperatura había caído a 109K, permitiendo así la fusión nuclear:
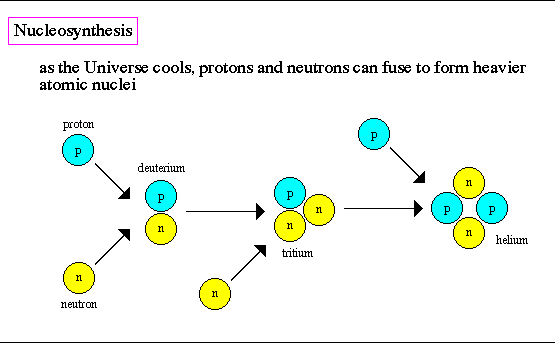
- Síntesis de Deuterio
La materia prima para la nucleosíntesis son los protones y neutrones. El primer paso es la fusión de un protón y un neutrón para formar Deuterio.
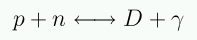
Como esta reacción es muy probable, la rápida expansión del Universo no logrará impedir que todos los neutrones se fusionen con los protones. La escasez inicial de neutrones (n/p=0.2) explican porqué el Universo dejó 75% de los protones en forma de Hidrógeno. Si bien los protones restantes pueden fusionarse para producir Deuterio, esta reacción es muy lenta y la expansión del Universo es muy rápida.
La temperatura Tnuc a la cual ocurre la nucleosíntesis de Deuterio es de Tnuc=7.6×108 K, a una edad de t~200 s.
- Síntesis de Helio
Una vez que se forman los núcleos de Deuterio, éstos pueden fusionarse para formar núcleos más complejos. Por ejemplo,
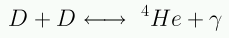
La probabilidad de esta reacción es alta, por lo que una vez que la nucleosíntesis comienza, los núcleos de D se convierten rápidamente en 4He.
- Síntesis de elementos más pesados
Los núcleos de 4He están fuertemente ligados por lo que la fusión de estos núcleos es poco probable. Sólo se forman pequeñas cantidades de 6Li y 7Li a través de las reacciones:

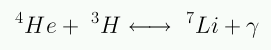
Para producir núcleos más pesados se requiere la interacción simultánea de 3 núcleos de 4He (reacción triple alfa). Esta reacción se ve muy dificultada debido a que la tasa de expansión del Universo es mucho mayor que la frecuencia de esa reacción (la densidad de los núcleos disminuye rápidamente). En resumen:
1) una vez que se comienza a formar Deuterio, la nucleosíntesis procede rápidamente para producir 4He.
2) La gran estabilidad del 4He impide mayor grado de nucleosíntesis y sólo se producen pequeñas cantidades de núcleos más pesados. La nucleosíntesis primordial queda muy incompleta.
- Modelo numéricos de nucleosíntesis primordial
La cantidad precisa de isótopos producidos en el Big Bang se puede calcular usando complejos códigos numéricos. Esta figura muestra la fracción de masa de distintos isótopos en función del tiempo :
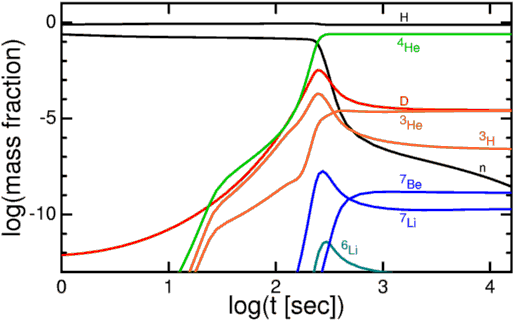
Inicialmente (T >> 109 K) casi toda la materia estaba en forma de neutrones y protones libres. Eventualmente la abundancia de D comienza a subir pero prontamente los núcleos de D se fusionan para formar 3H, 3He y 4He. El D alcanza un máximo cerca de 109 K y luego decrece. Cuando la temperatura ha caído a 4×108 K (t~10 min) la nucleosíntesis ha cesado. El resultado de la nucleosíntesis primordial es:
- 76% de los bariones en forma de protones libres (H)
- 24% de los bariones en forma de 4He
- 4×10-5 de los bariones en forma de D
- 10-5 de los bariones en forma de 3He
- 10-9 de los bariones en forma de 7Be
- 10-10 de los bariones en forma de 7Li
Estas abundancias coinciden con los valores medidos!, lo cual aporta una fuerte evidencia al modelo del Big Bang.
- La abundancia de los elementos químicos más livianos (hidrógeno y helio) se puede
explicar debido a la fusión nuclear cuando el Universo era joven, denso y caliente
(animación).
- 3. El Fondo de Radiación Cósmico (CMB)
- El modelo de Big Bang de Gamow et al. predice que en el Universo temprano
la materia se encontraba ionizada y en equilibrio con la radiación (con un espectro de
cuerpo negro). A medida que la expansión prosiguió y que la temperatura
había disminuído a unos 4000 K, los núcleos atómicos pudieron comenzar
a combinarse con los electrones libres para formar átomos neutros, lo cual
se denomina época de recombinación. Esto ocurre
cuando el Universo tenía 350.000 años.
Antes de la recombinación los fotones y los electrones interactuaban frecuentemente de modo que la radiación tenía un espectro de cuerpo negro a la temperatura de la materia. Luego de la recombinación los fotones cesan de interactuar con la materia. Esto se denomina época de desacoplamiento, la cual ocurre inmediatamente después de la recombinación. En este momento el Universo se hace transparente para la radiación. Desde la época de desacoplamiento la radiación de cuerpo negro se ha estado enfriando debido a la expansión y hoy el Universo debe estar lleno de radiación fósil con una temperatura de 5 K.
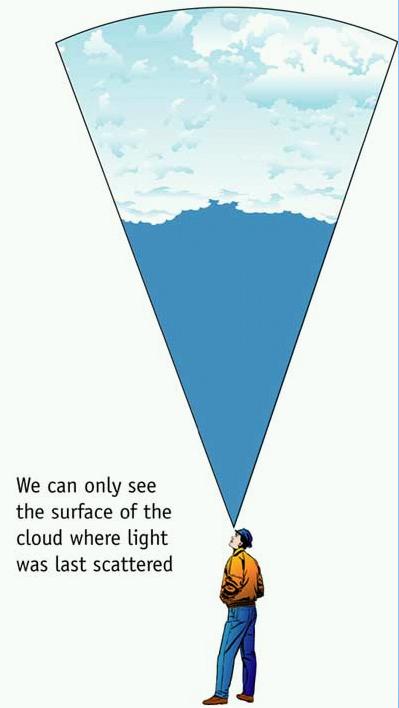
- Observaciones del Fondo de Radiación Cósmico
El CMB fue descubierto accidentalmente en 1965 por los ingenieros Penzias y Wilson del Bell Telephone Laboratories usando una radio antena en 7.35 cm. Al apuntar la antena al cielo encontraron una señal más alta de lo esperado, isotrópica y correspondiente a una temperatura de 3.5 K.

Esta emisión era la radiacion cósmica de cuerpo negro propuesta en 1948 por Gamow, Alpher y Herman!
El CMB es muy difícil de observar desde la superficie de la Tierra debido a la opacidad de la atmósfera. La primera medición precisa del CMB fue realizada por el satélite COBE entre 1989-1992 a longitudes de onda 0.1-10 mm.
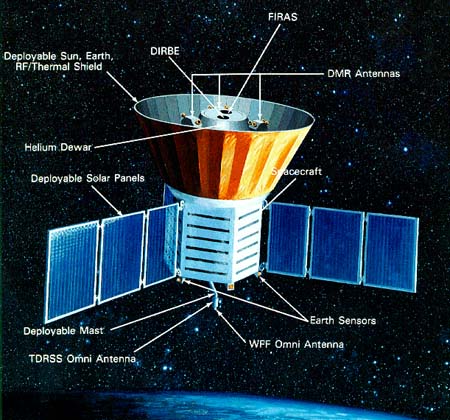
COBE mostró que el CMB tiene un espectro de un cuerpo negro con T=2.725 K:
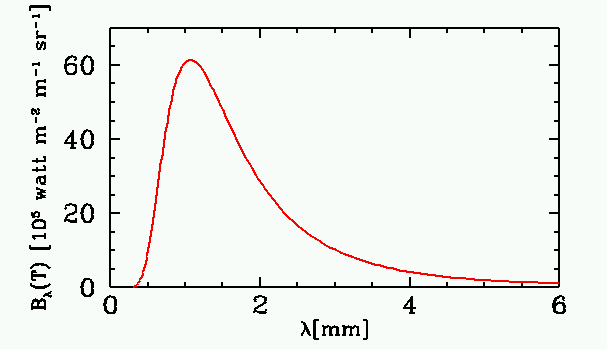
El CMB es MUY uniforme, aunque no perfectamente uniforme. La magnitud de las variaciones de temperatura en el cielo son ΔT/T∼10-5 o solo 30 microKelvin. Esto demuestra la gran isotropía del Universo.
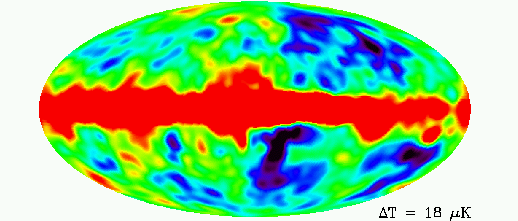
- Una radiación de fondo de cuerpo negro tan isotrópica es el resultado natural de un Universo que fue denso, caliente, opaco y homogéneo en el pasado, y constituye una confirmación del modelo del Big Bang caliente de Lemaître y Gamow. El CMB constituye la tercera evidencia observacional contundente en favor del Big Bang. Los hallazgos del COBE acaban de valerle el Premio Nobel de Física 2006 a John Mather y George Smoot.
- Luego del divorcio de bariones y fotones, los bariones quedan libres del acecho de los fotones y comienzan a gozar de la libertad para colapsar por su propia gravedad (y la gravedad de la materia no bariónica) y formar galaxias, estrellas, planetas, y astrónomos. El CMB revela las condiciones iniciales que tenían los bariones para la formación de estructuras en el Universo y su estudio es el punto de partida para comprender cómo se formaron dichas estructuras. El CMB es una imagen de este importante hito en la infancia del Universo.
II. Dinámica Cósmica En estricto rigor es necesario usar la teoría de la RG para describir la dinámica cósmica. Sin embargo, es posible entender la expansión usando la teoría de Newton sin incurrir en complicaciones matemáticas.
- El modelo de Big Bang de Gamow et al. predice que en el Universo temprano
la materia se encontraba ionizada y en equilibrio con la radiación (con un espectro de
cuerpo negro). A medida que la expansión prosiguió y que la temperatura
había disminuído a unos 4000 K, los núcleos atómicos pudieron comenzar
a combinarse con los electrones libres para formar átomos neutros, lo cual
se denomina época de recombinación. Esto ocurre
cuando el Universo tenía 350.000 años.
- 1. Cosmología newtoniana
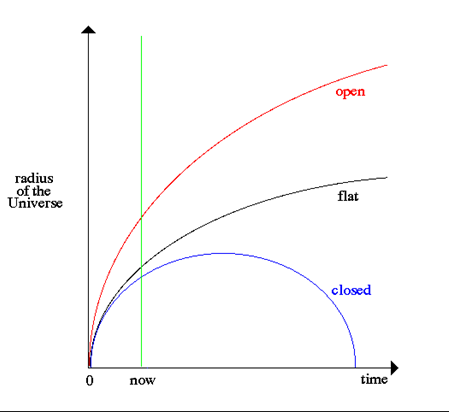
- Si U>0 ⇒ da/dt>0 ⇒ da/dt nunca llega a cero. Un universo con (da/dt)(t=t0)>0 siempre se expandirá.
- Si U<0 ⇒ existe amax tal que da/dt=0; amax=√-Ur/GM. En algún momento la expansión se detendrá. Como d2a/dt2 < 0, la expansión se convertirá en contracción.
- Si U=0 ⇒ a medida que a(t) → ∞, ρ(t) → 0 ⇒ da/dt → 0 para t → ∞
Supongamos un universo homogéneo e infinito, consideremos una esfera dentro del Universo, y estudiemos el movimiento de una partícula de masa m sobre la superficie de la esfera.
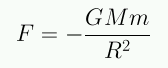
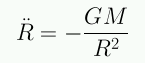
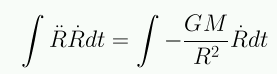

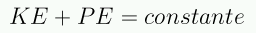
La masa dentro de la esfera es constante:

Para una expansión isotrópica el radio de la esfera debe aumentar de la forma:
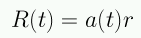
en que r es el radio comóvil y a(t) es el factor de escala (adimensional). Por convención en la actualidad (t=t0), a(t=t0)=1. Así la ecuación que describe la dinámica cósmica queda de la siguiente forma:
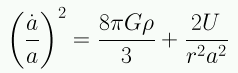
Esta es la "Ecuación de Friedmann" en honor a quien la dedujera por primera vez a partir de la RG en 1922. Esta ecuación de Friedmann admite 3 tipos de soluciones:
Los 3 destinos posibles de la esfera en un Universo newtoniano son análogos a la suerte de una piedra lanzada hacia arriba.
- 2. Forma correcta de la ecuación de Friedmann
- ε contiene todas las componentes de energía del Universo (materia común, fotones, neutrinos, y
otras formas mas exóticas de energía), e incluye la masa en reposo y el momentum de las partículas.
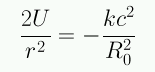
- La energía U corresponde a la curvatura del espacio, la cual queda definida
completamente por el radio de curvatura R0 (en unidades de distancia) y el parámetro de curvatura
que admite tres posibles valores: k=-1,0,1.
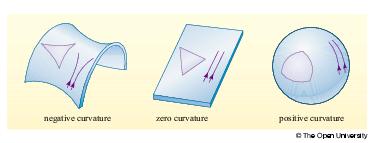
Esta figura muestra los tres tipos de espacios curvos posibles en 2D para un Universo sin centro: espacios con curvatura negativa (k=-1), planos (k=0), y con curvatura positiva (k=+1). - Si Ω < 1, k=-1
- Si Ω = 1, k= 0
- Si Ω > 1, k=+1
Aplicando la ecuación de campo de Einstein a un universo homegéneo e isotrópico se llega a la ecuación de Friedmann derivada en 1922:
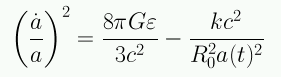
Definiendo el parámetro de Hubble como una medida de la tasa de variación del factor de escala:
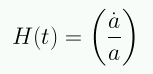
la ecuación de Friedmann queda:
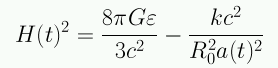
La ecuación de Friedmann relaciona la curvatura (k y R0), la tasa de expansión H(t), y la densidad de energía ε.
Para un universo plano (k=0):
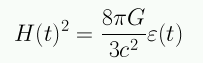
Dado H(t) hay una densidad crítica:
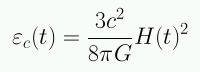
En el instante actual:
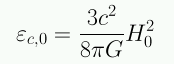
Para H0=70 km s-1 Mpc-1 la densidad de energía crítica es de 6 protones m-3.
En la discusiones de curvatura habitualmente se usa el parámetro de densidad (adimensional):
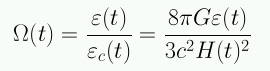
En términos del parámetro de densidad la ecuación de Friedmann se escribe:
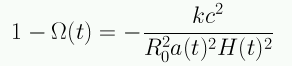
Se puede ver que el parámetro de densidad define la geometría del Universo:
En el momento actual
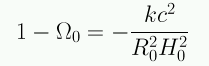
Si logramos medir Ω0, podemos conocer la geometría del Universo!
- ε contiene todas las componentes de energía del Universo (materia común, fotones, neutrinos, y
otras formas mas exóticas de energía), e incluye la masa en reposo y el momentum de las partículas.
- 3. Solución a la ecuación de Friedmann para un universo plano (k=0)
Un universo plano sólo con materia se denomina Einstein-de Sitter. Este modelo era el estándar en la década de 1990. Es este caso la ecuación de Friedmann se reduce a:
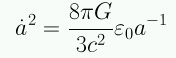
La solución para este caso es:
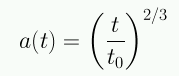
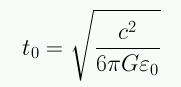
Podemos calcular la constante de Hubble:
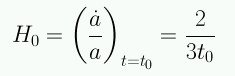
la cual permite obtener la edad del Universo. Para el caso H0=70, t0=9.3 Gyrs.
En general, el factor de escala dependerá de los componentes de energía del Universo y se puede calcular integrando numéricamente la ecuación de Friedmann:
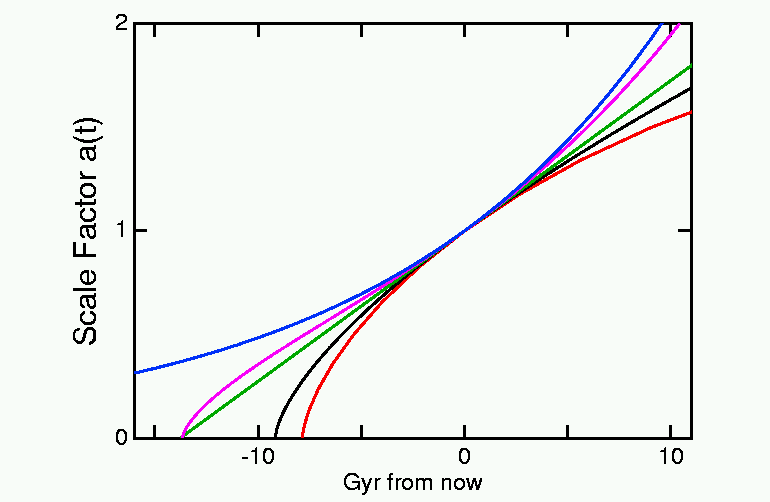
Si lográramos medir a(t) podríamos saber cuál es la densidad de energía y la geometría del Universo. Desafortunadamente no es posible medir a(t), pero sí podemos medir el redshift de distintas fuentes (galaxias). De acuerdo a la definición de redshift, esta cantidad mide el cambio entre la longitud de onda emitida y la longitud de onda recibida:
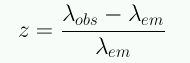
Como todas la longitudes se estiran a medida que el Universo se expande, las ondas también se estiran de modo que el redshift está relacionado con el factor de escala:
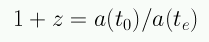

Al observar un objeto de redshift z=3, estamos viendo luz que fue emitida cuando el universo tenía un factor de escala a=1/4.
El redshift hace que el espectro se desplace al rojo y se estire:
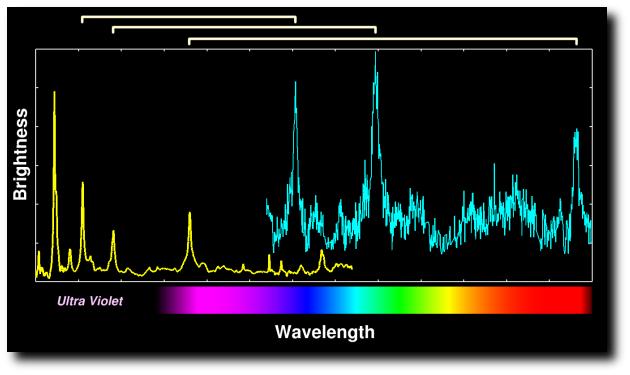
Espectro de un cuasar en reposo y otro corrido al rojo

Otra cantidad observacional es la distancia. Dependiendo de la geometría del Universo podemos calcular el camino recorrido por un fotón entre la emisión y la recepción y el instante en el cual el fotón salió. Si logramos medir distancias y redhifts podremos reconstruir a(t) y saber la geometría y el destino del Universo.
- 4. Test cosmológico en base a distancias y redshifts
Para saber si realmente vivimos en un universo plano tenemos que tratar de medir la historia de la expansión cósmica, a(t), y deducir el valor de Ω que mejor se ajusta a las observaciones. Por un lado el redshift nos dice el valor de a(t) cuando la luz de la fuente fue emitida. Por otro lado la distancia a la fuente nos dice el instante en el cual los fotones fueron emitidos. Al combinar medidas de (d,z) podemos deducir a(t) y el valor de Ω.
Los mejores indicadores de distancia son las supernovas de tipo Ia las cuales han permitido medir distancias hasta redshifts de z=1.7. El método consiste básicamente en usar la ley del inverso del cuadrado:
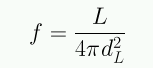
en que L es la luminosidad de la supernova, f es el flujo medido por el observador y dL es la distancia entre la supernova y el observador.
Este método requiere conocer la luminosidad intrínseca de las supernovas. La calibración de las luminosidades fue realizado en Chile entre 1990-1993 durante el proyecto Calán/Tololo. A partir de 1995 dos grupos de astrónomos internacionales comenzaron a buscar supernovas lejanas. Aplicando la calibración del proyecto Calán/Tololo, en 1998 obtuvieron el siguiente diagrama:
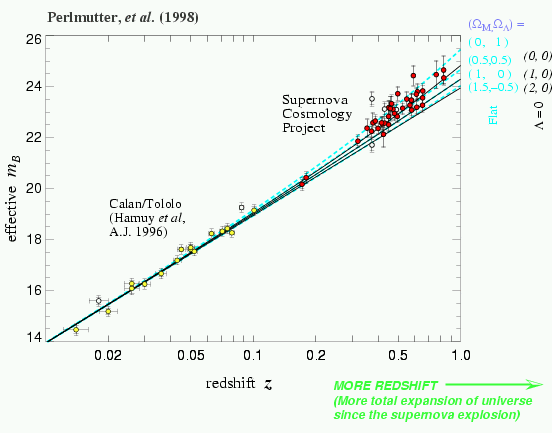
El eje vertical es una medida logarítmica del flujo de las supernovas, es decir, una medida logarítmica de sus distancias. Las curvas de color negro son modelos para distintos valores de Ω=0,1,2.
Cada punto en el diagrama corresponde a una supernova. El conjunto de puntos no es consistente con ninguno de estos valores. Peor aún, estas observaciones sugieren una densidad de masa negativa!
Para poder ajustar las observaciones se requiere introducir una nueva componente de energía que actúe como "anti-gravedad". La hipótesis más económica apela a una energía del espacio vacío denominada constante cosmológica (Λ)
Estas observaciones sugieren que la energía asociada a la constante cosmológica tiene un parámetro de energía de ΩΛ,0=0.7 mientras que la materia tiene sólo Ωm,0=0.3. Curiosamente, la energía total del Universo es Ω=ΩΛ,0+Ωm,0=1, es decir, el Universo tiene geometría plana.
El efecto de la constante cosmológica supera a la fuerza gravitacional de la materia del Universo causando una expansión acelerada! Este descubrimiento ha remecido las bases de la física. Fue considerado por la revista Science como el resultado científico más importante del año 1998:

mhamuy@das.uchile.cl